The gas laws

We live in an invisible sea of gases that make up the our rather thin but life sustaining atmosphere. Many of the physical properties of gases such as the relationships between their pressure, volume and temperature were investigated by amateur but enthusiastic scientists using rather crude apparatus in the 17th-19th centuries. Through a series of simple but ingenious experiments they were able to derive a set of laws linking pressure, temperature, volume and amount of gas present. These laws are called the gas laws.

Boyle's law- The relationship between pressure and volume (constant temperature)

Robert Boyle was a scientist who believed in investigating science through experimental methods. He carried out the experiment shown below to investigate the relationship between the pressure and volume of a gas.

Here some simple glass u-tubes were filled with liquid mercury. The tubes were sealed at one end. He measured how the volume of trapped gas changed as he added mercury columns of various heights. Throughout his experiments the temperature and amount of gas present were kept constant.

Apparatus used to investigate Boyles's law

What Boyle found was that as the pressure increased the volume decreased e.g. as the pressure was double the volume halved , or if the volume of the gas increases by a factor of 5, then the pressure has decreased to a 1/5 of what it was previously. This means that the volume of the gas is inversely proportional to the pressure. The image below summarises the relationship between the pressure and volume of a gas.

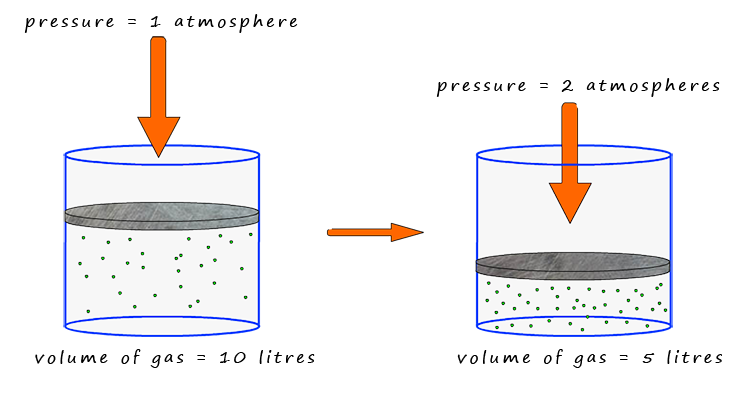
This means that the pressure p, multiplied by the volume V is always a constant.

pV= constant(k)

or

pV= k

if the change the pressure and the volume of the gas then the new pressure, p₂ multiplied by the new volume V₂ will still equal the constant K as long as the temperature and amount of gas present do not change..

p₂V₂ = k

So we can write:

pV = k = p₂V₂

p₁V₁ = p₂V₂

Finding the value of the constant k

Graph showing how pressure and volume vary- Boyle's law

The value of the constant k depends on the temperature and the amount of gas present (number of moles of gas) . However if a graph of V versus 1/p is plotted then the gradient of the line produced will provide the value of k.

Charles's Law, the temperature-volume relationship

As the temperature(T) of a fixed mass (n) of gas at constant pressure (p) increases it expands in a linear fashion. That is:

V= constant x T

V/T = constant

A simple diagram to help explain Charles law is shown below. Here a fixed mass of gas is placed inside a sealed container with a movable piston/plunger on top. The container should have a scale on it to indicate the volume of the gas inside it. The gas is heated to a known temperature, this will cause it to expand and its new volume can be read from the scale on the container.

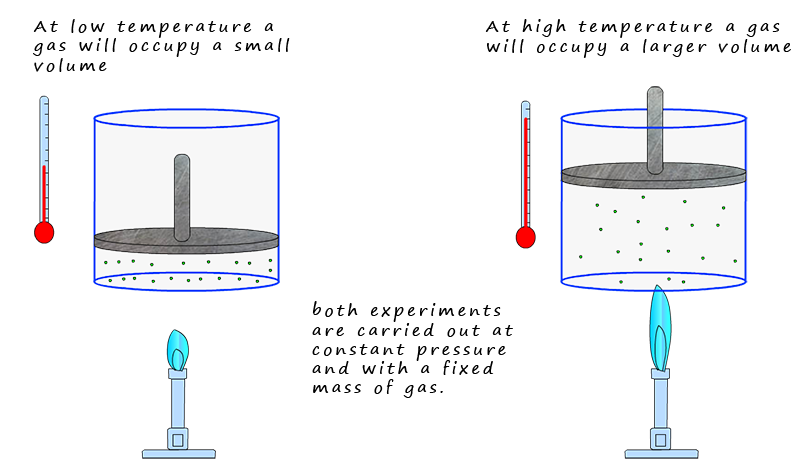
Charles Law, relating volume and temperature of a gas

By taking many volume and temperature reading the following is found:

V/T = constant (k)

Since at a new temperature (T₂) and a new volume (V₂) the ratio of

V₂/T₂ =constant (k)

Then:

V₁/T₁= V₂/T₂

As an everyday example of Charles's Law in action think of a balloon. The number of moles of air inside the balloon is fixed. If the balloon is warmed gently then the air inside will heat up and the balloon will expand. Cooling the balloon will also cause the volume of the air to shrink inside it. This basic principle is used inside hot air balloons, where the air expands when heated and the density drops inside the balloon, but the air is still at the same pressure as the air outside the balloon.

Avogadro's Hypothesis

In 1811 Amedeo Avogadro proposed what is now called Avogadro's Hypothesis. He proposed that: Equal volumes of gases at the same temperatur and pressure contain equal numbers of particles. At 273k or 0⁰C and 101kPa for example 1 mole of any gas will occupy a volume of 22.4 litres or 22.4 dm³. These conditions of temperature and pressure are called standard temperature and pressure (S.T.P). At 298K (25⁰C) and 101kPa 1 mole of any gas will occupy 24 litres or 24 dm³; these conditions are called room temperature and pressure.
avogadro's law

The ideal gas equation

So far we have:

Boyles's law : V ∝ 1/p (constant n,T)

Charles's law : V∝ T (constant n, p)

Avogadro's law : V ∝n (constant p, T)

We can combine these 3 gas laws into one general equation:

V ∝ nT/p

We can also write this as:

V=R(nT/p) where R is a constant

We can rearrange this to give:

PV = nRT

This equation is called the ideal gas equation. The term R is called the gas constant and its units will depend upon the units of p,T and V, though the temperature must always be in degrees Kelvin. However when V is in cubic metres (m³), T in Kelvins (K), pressure in pascals (Pa) the value of R is 8.31 JK^-1mol^-1, these are the systeme Internationale (SI units) for p, T, n and V.