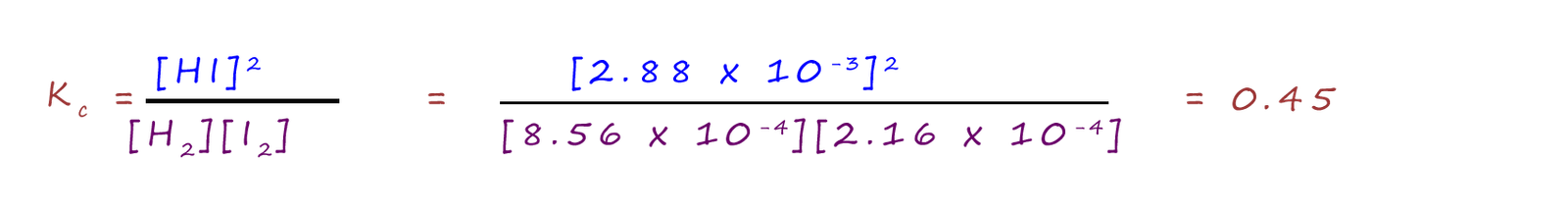
For any reversible reaction at equilibrium, such as:

Kc is the equilibrium constant and the subscript c refers to concentration of the reactants and products in mol dm-3. The square brackets [] are used to indicate that we are using concentrations in mol dm-3 for all of the reactants and products.
As an example consider the Haber process for making ammonia. The best place to start when working out the value for equilibrium constant is by writing a balanced equation symbolic equation for the reaction and then from this we can write an expression for the equilibrium constant Kc.
An equation for the Haber process is shown below:
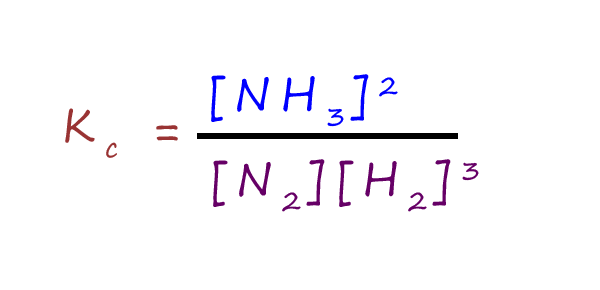
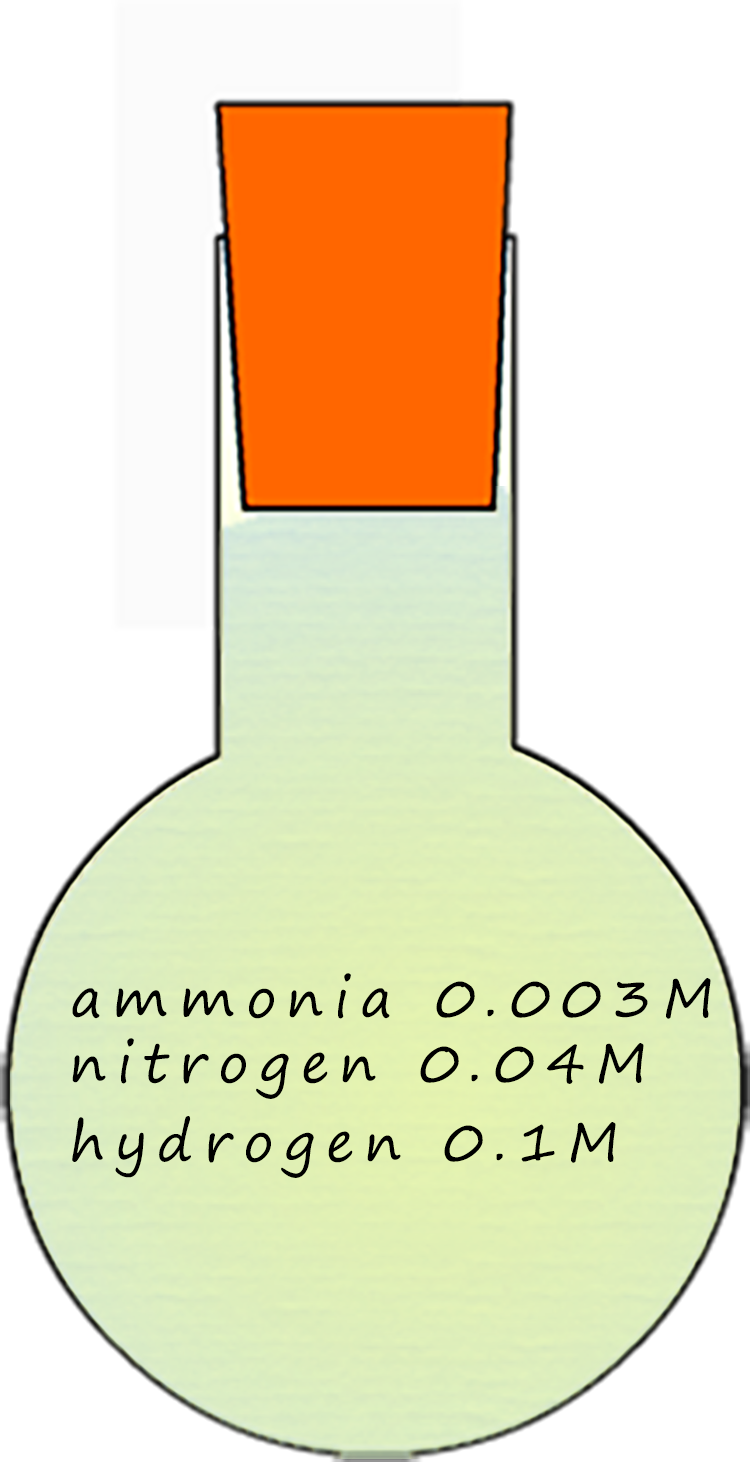
Suppose we have a flask filled with an equilibrium mixture of nitrogen, hydrogen and ammonia. The equilibrium mixture contains the three gases with the following concentrations:
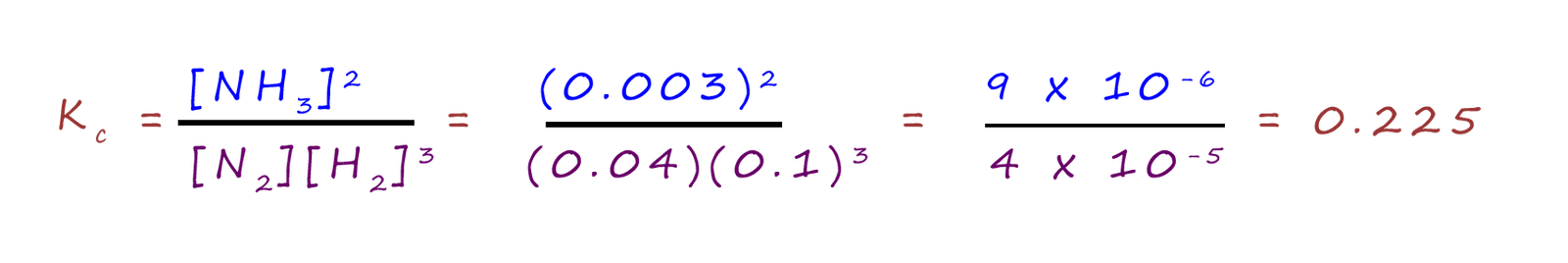
The equilibrium constant Kc value of 0.225 is a small number indicating that the equilibrium mixture contains little ammonia and the position of equilibrium lies to the left.
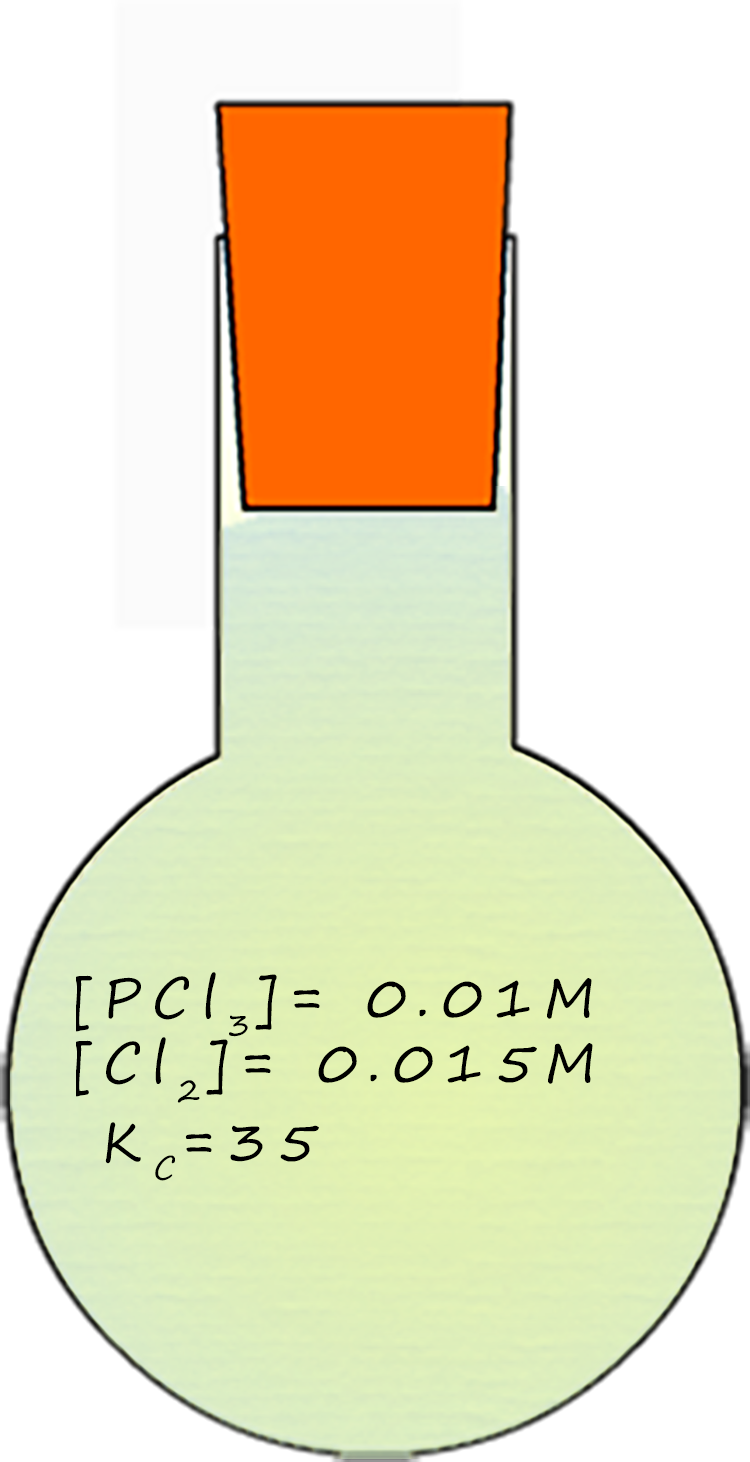
Phosphorus pentachloride (PCl5) can be prepared by reacting phosphorus trichloride (PCl3) with chlorine gas (Cl2) according to the equation below:
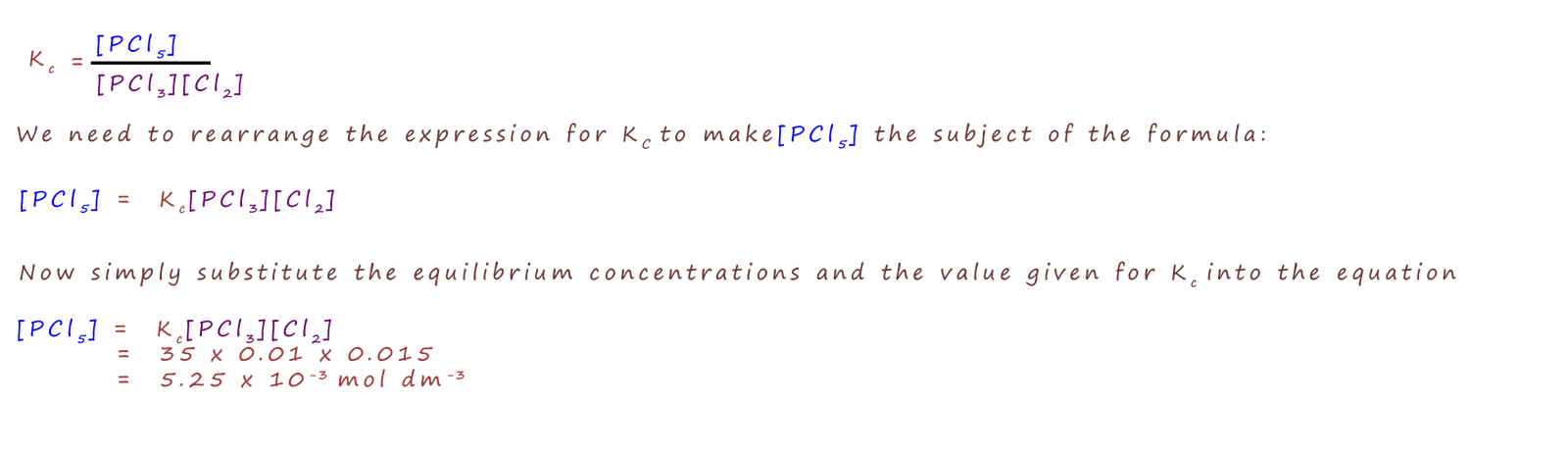
You may remember from your gcse lessons that esters are made by reacting a
carboxylic acid with an alcohol.
The ester ethyl ethanoate is made by the reaction of the alcohol ethanol with the
ethanoic acid. An equation for this
esterification reaction is given below:
Calculate the equilibrium constant Kc when 0.25 moles of ethanol
and
ethanoic acid are mixed together with a few drops sulfuric
acid catalyst in a
sealed flask. The reaction is heated to a constant temperature and allowed to reach equilibrium. The total volume
of
the system is 50ml and at equilibrium
it was found by titration that there was 0.0825 moles of ethanoic acid present.
The best way to tackle this type of product is by drawing up a table similar to the one below; it is often called an ICE table (Initial, change, equilibrium). You should use this table or one similar to it to record and work out all the concentration of the reactants and products before the reaction starts and after it has reached equilibrium. You can also use it to work out how the concentration of the reactants and products change during the reaction.
| reactants and products | ethanol | ethanoic acid | ethyl ethanoate | water |
|---|---|---|---|---|
| initial concentration (mol dm-3) | ||||
| change in concentration (mol dm-3) | ||||
| equilibrium concentration (mol dm-3) |
Initially we have the following:
At equilibrium we know that there is 0.0825 mol of ethanoic acid present. Initially there was 0.25 mol of ethanoic acid present so:
Since mole of acid reacts with 1 mole of ethanol, then we can say that: 0.25mol -0.0825mol = 0.1675mol of ethanol also reacted.
From the stoichiometry of the equation we know that 1 mole of acid reacts with 1 mole of ethanol to produce 1 mole of the ester and 1 mole of water. Since 0.1675 moles of acid and alcohol reacted we know that this will produce 0.1675 moles of ester and 0.1675 moles of water.
So at equilibrium we have:
All that is needed to calculate Kc is to convert the number of moles for each reactant and product at equilibrium into concentrations. This is easily done using the formula below, since we know the total volume of the system was 50ml or 0.05dm-3.
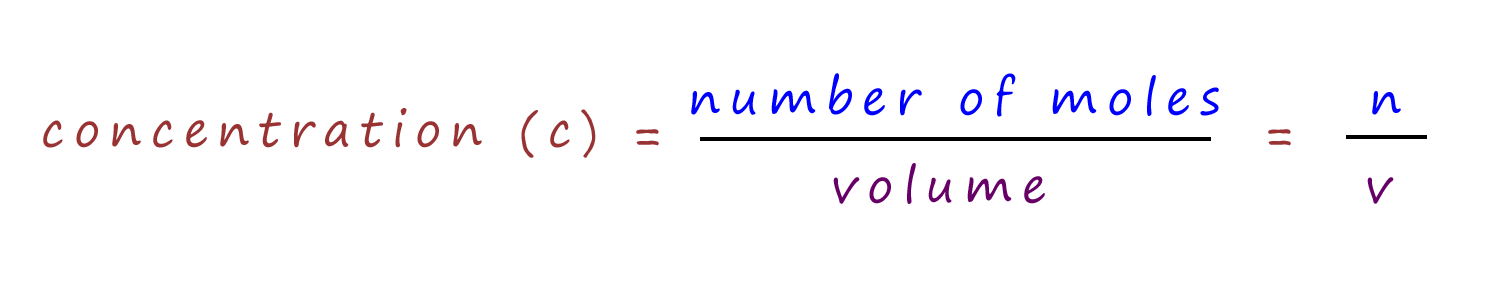
This gives equilibrium concentrations of:
We can now fill in our ICE table using the calculate concentrations from above:
| reactants and products | ethanol | ethanoic acid | ethyl ethanoate | water |
|---|---|---|---|---|
| initial concentration (mol dm-3) | 0.25/0.05 =5 | 0.25/0.05 =5 | 0 | 0 |
| change in concentration (mol dm-3) | -3.35 | -3.35 | +3.35 | +3.35 |
| equilibrium concentration (mol dm-3) | 0.0825/0.05=1.65 | 0.0825/0.05=1.65 | 0.1675/0.05=3.35 | 0.1675/0.05=3.35 |
To calculate Kc it is simply a matter of substituting the values for the concentrations of the reactants and products into the expression for the equilibrium constant:
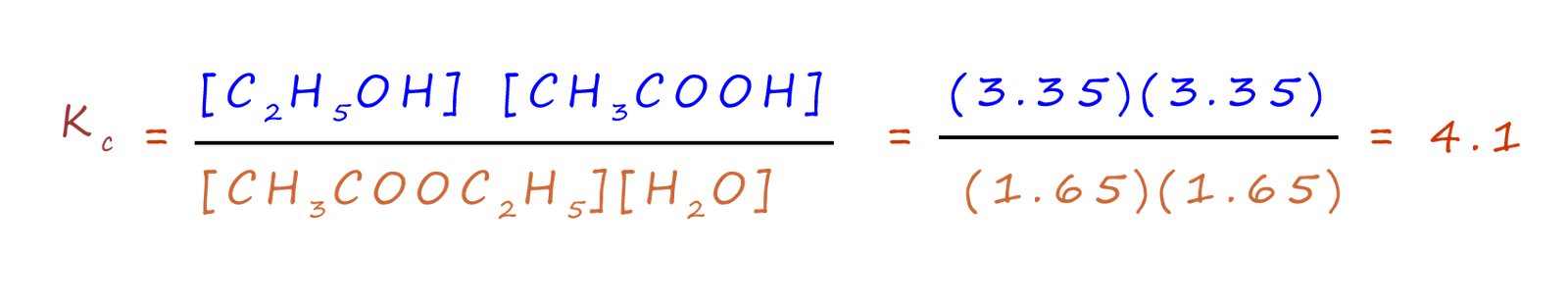
As a variation on the ester example above suppose you mixed together 1 mol of ethanoic acid and 1 mol of ethanol and you wanted to know how much ester you would have at equilibrium. We already know Kc for the reaction and we also know the stoichiometry of the reaction.
Recall that Kc requires concentrations, however we have the number of reacting moles. Suppose the volume of the equilibrium mixture was V dm-3, then we have:

so at equilibrium we have 0.67 moles of ester and water and 0.33 moles of ethanoic acid and ethanol in the equilibrium mixture.
You could be asked to calculate an equilibrium constant
for a reaction when not all the equilibrium
concentrations are known.
However as long as we know the concentration
of the reactants and the equilibrium
concentration of at least one of the
reactants or products then it is possible
to calculate the equilibrium constant, Kc for the reaction.
As an example consider the reaction of hydrogen and iodine to form hydrogen iodide. The equation of the reaction is shown below:
Example:
A mixture of 5 x 10-3 mol of hydrogen gas and 1.8 x 10-3 mol of iodine were placed in a flask with a volume of 5 dm-3. The flask was heated to a known temperature and allowed to reach equilibrium. At equilibrium the [HI] was found to be 2.88 x 10-4 mol dm-3. Calculate Kc for this reaction.
| reactants and products | H2 | I2 | HI |
|---|---|---|---|
| initial concentration (mol dm-3) | |||
| change in concentration (mol dm-3) | |||
| equilibrium concentration (mol dm-3) |
Remember that when using Kc the "c" refers to concentration in mol dm-3, however in the problem above we are only given moles and not concentrations. So the first step is to calculate the concentrations from the values given. The concentration is found using the formula:
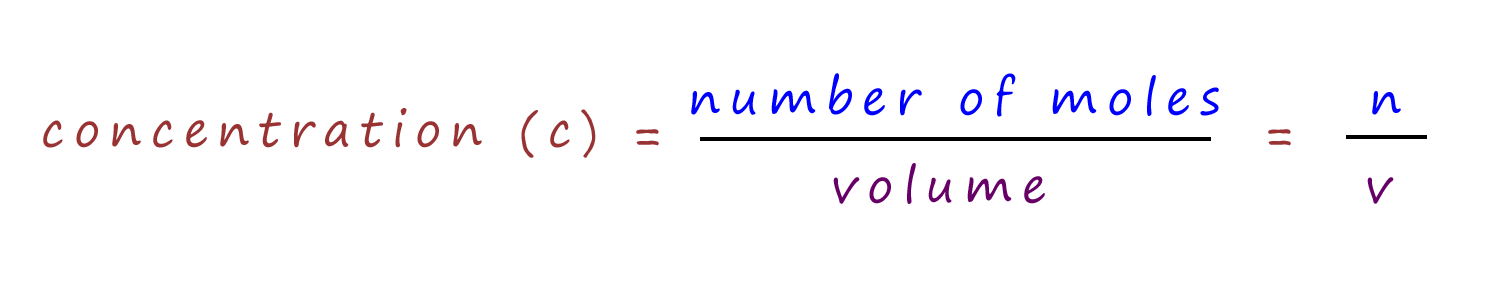
So simply substitute the values for the number of moles of iodine and hydrogen into the equation to obtain their concentrations in mol dm-3:
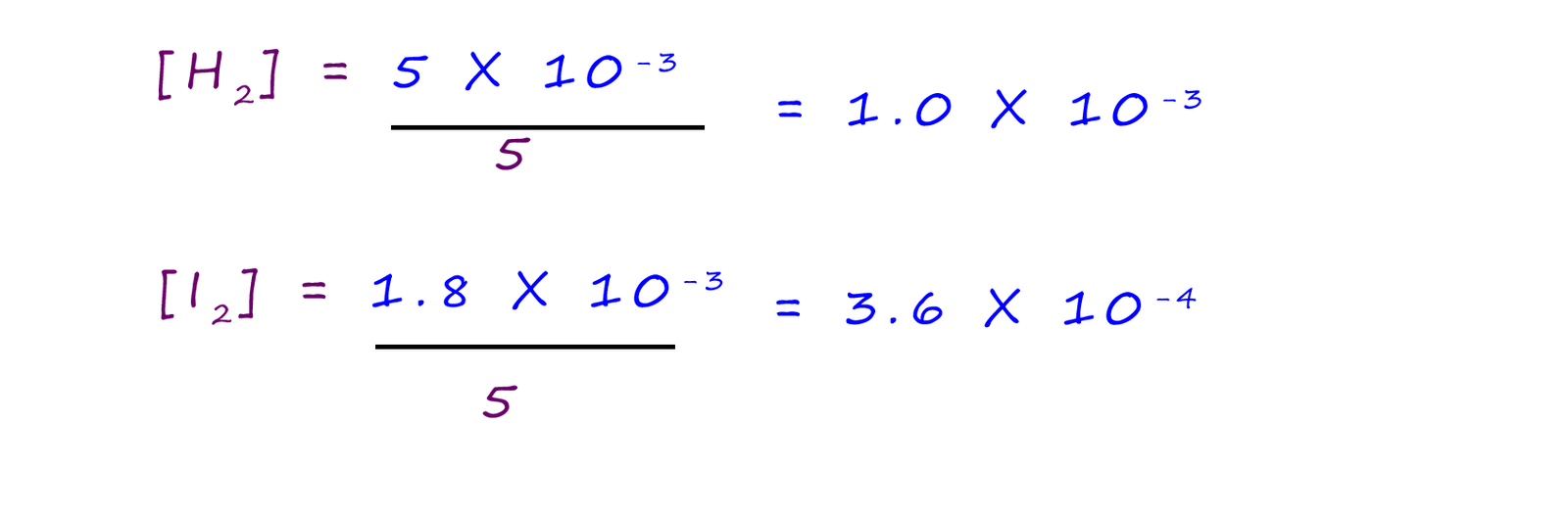
Now fill in the table with all known values of concentration:
| reactants and products | H2 | I2 | HI |
|---|---|---|---|
| initial concentration (mol dm-3) | 1.0 x 10-3 | 3.6 x 10-4 | |
| change in concentration (mol dm-3) | |||
| equilibrium concentration (mol dm-3) | 2.88 x 10-4 |
The next step in finding the equilibrium constant, Kc is to calculate the equilibrium concentrations for hydrogen and iodine. This is easily done.
We need to consider the stoichiometry of the equation for the reaction:
| reactants and products | H2 | I2 | HI |
|---|---|---|---|
| initial concentration (mol dm-3) | 1.0 x 10-3 | 3.6 x 10-4 | 0 |
| change in concentration (mol dm-3) | -1.44 x 10-4 | -1.44 x 10-4 | +2.88 x 10-4 |
| equilibrium concentration (mol dm-3) | 8.56 x10-4 | 2.16 x 10-4 | 2.88 x 10-4 |
Substituting the equilibrium concentrations into the expression for Kc gives: