The equilibrium constant (K_c)

A reversible reaction is one that does not go to completion, so instead of everything turning into products we are left with a mixture of reactants and products. In a closed system, the reaction can reach dynamic equilibrium, where both the forward and reverse reactions are still happening, but at the same rate.

You have already met Le Chatelier's principle, which is really useful for predicting the direction an equilibrium will shift when conditions such as temperature, pressure or concentration are changed. However, Le Chatelier's principle does not tell you how much of each reactant and product will be present once equilibrium is re-established.

Equilibrium constants (K_c)

This is where equilibrium constants come in. Rather than just telling us which direction the equilibrium lies, the equilibrium constant (K_c) allows us to put a number on the position of equilibrium. On this page, we will look at how the equilibrium constant (K_c) is used in practice. We will also look at:

• How to write expressions for equilibrium constants from balanced chemical equations
• What the value of the equilibrium constant (K_c) tells us about the position of equilibrium
• How to work out the units of the equilibrium constant (K_c)
• Why the value of the equilibrium constant (K_c) only changes when the temperature is changed

Expressions for the equilibrium constant, K_c

Consider a reaction that we are all familiar with; the Haber process for the synthesis of ammonia gas:

Nitrogen_(g) + hydrogen_(g) ⇌ ammonia_(g)

N_2(g) + 3H_2(g) ⇌ 2NH_3(g)

Now imagine setting up several flasks containing different amounts of nitrogen, hydrogen and ammonia, as shown in the image below. Even though the starting composition in each flask is different, if all the flasks are kept at the same temperature and allowed to reach equilibrium, something interesting happens...

So you are probably wondering what happens. Well we can say that:

The equilibrium constant (K_c)

At this point you might be wondering where the ratio [NH₃]² / ([N₂][H₂]³) actually comes from. The key to answering this is to look back at the balanced chemical equation for the synthesis of ammonia. If you compare the numbers in the equation with the powers in the ratio, you should start to see the connection. This idea is not unique to the Haber process; in fact, we can say that in general for any reversible reaction at equilibrium:

aA_(aq) + bB_(aq) ⇌ cC_(aq) + dD_(aq)

Where A, B and C, D are the reactants and products, while a, b, c and d are the coefficients in the balanced equation. The expression for the equilibrium constant (K_c) for this reaction is given by:

K_c is the equilibrium constant and the subscript c refers to concentrations in mol dm^-3. The square brackets [ ] are used to indicate that we are using concentrations in mol dm^-3 for all of the reactants and products. The equilibrium constant is a ratio of the concentration of the products over the reactants, with each reactant and product concentration raised to the power of the coefficients in the balanced equation. So for the Haber process we can write:

The Haber process for making ammonia

N_2(g) + 3H_2(g) ⇌ 2NH_3(g)

This gives an expression for the equilibrium constant for the Haber process of:

The equilibrium constant is easily written from the balanced symbolic equation. For example consider the formation of sulfur trioxide gas from sulfur dioxide:

The synthesis of sulfur trioxide gas

2SO_2(g) + O_2(g) ⇌ 2SO_3(g)

This gives an expression for the equilibrium constant for the formation of sulfur trioxide of:

As a final example consider the formation of hydrogen iodide gas from gaseous hydrogen and iodine; an equation for this reaction is shown below:

H_2(g) + I_2(g) ⇌ 2HI_(g)

This gives an expression for the equilibrium constant for the formation of hydrogen iodide of:

The units of the equilibrium constant

The units of the equilibrium constant depend upon the stoichiometry (number of reacting moles) of the equation. For example consider the following reaction:

A_(g) + B_(g) ⇌ C_(g)

An expression for the equilibrium constant with units is shown below. Remember that for the equilibrium constant K_c all concentrations must be in mol dm^-3. To work out the units of K_c replace each concentration term in the expression for k_c with its units (mol dm^-3) and then cancel out identical terms on the top and bottom lines just like algebra, this is outlined in the three examples below:

Example 2: Consider the following reaction:

2A_(g) + B_(g) ⇌ C_(g)

This time in the equilibrium expression for A we have [A]². We square the units of concentration:
(mol dm^-3)(mol dm^-3) = (mol² dm^-6).
As before, cancel out identical units from the top and bottom lines. The expression and units for the equilibrium constant (K_c) is:

Example 3: Consider the following reaction:

A_(aq) + B_(aq) ⇌ C_(aq) + D_(aq)

The expression to work out the units for K_c is:

Heterogeneous equilibria and solids in K_c

So far all of the examples we have looked at involve reactions where all of the reactants and products are gases or aqueous solutions. These are examples of homogeneous equilibria.

However, many equilibrium reactions involve substances in different physical states such as solids and gases. These are called heterogeneous equilibria.

For example, consider the following equilibrium:

CaCO_3(s) ⇌ CaO_(s) + CO_2(g)

Although this equation contains three substances, only carbon dioxide is a gas. The solids calcium carbonate and calcium oxide are not included in the equilibrium expression.

This is because the concentrations of pure solids do not change during the reaction, so they have no effect on the value of K_c.

As another example consider the decomposition of solid ammonium chloride to form gaseous ammonia and hydrogen chloride gas:

NH₄Cl_(s) ⇌ NH_3(g) + HCl_(g)

Here, the solid ammonium chloride is omitted, so the expression for the equilibrium constant is simply:

Whenever you write an expression for K_c always start by crossing out any solids or pure liquids in the balanced equation.

The values of the equilibrium constants

Since the value of the equilibrium constant (K_c) is the ratio of the concentration of the products over the reactants its value will give an excellent indication of whether there is more reactant or product present at equilibrium. The values of K_c vary tremendously; from very large numbers (for example 1 x 10⁵⁰) to very small numbers (such as 1 x 10^-20). These numbers give us a good indication of what is happening at equilibrium:

• If K_c is large (for example 100 or 1 x 10¹⁰) then there is much more product than reactant in the equilibrium mixture. The larger the value of K_c the more products and the fewer reactants are present. We would say the position of equilibrium lies to the right (that is towards the products).
• If K_c is small (for example 0.0011 or 1 x 10^-5) then there is much less product than reactant in the equilibrium mixture. The smaller the value of K_c, the more reactant and the fewer products are present. We would say the position of equilibrium lies to the left (that is towards the reactants).
• If K_c is not particularly large (maybe close to 1), then it is likely that there are approximately equal amounts of reactants and products in the equilibrium mixture.

This is summarised in the diagram below:

Equilibrium constants and Le Chatelier's principle

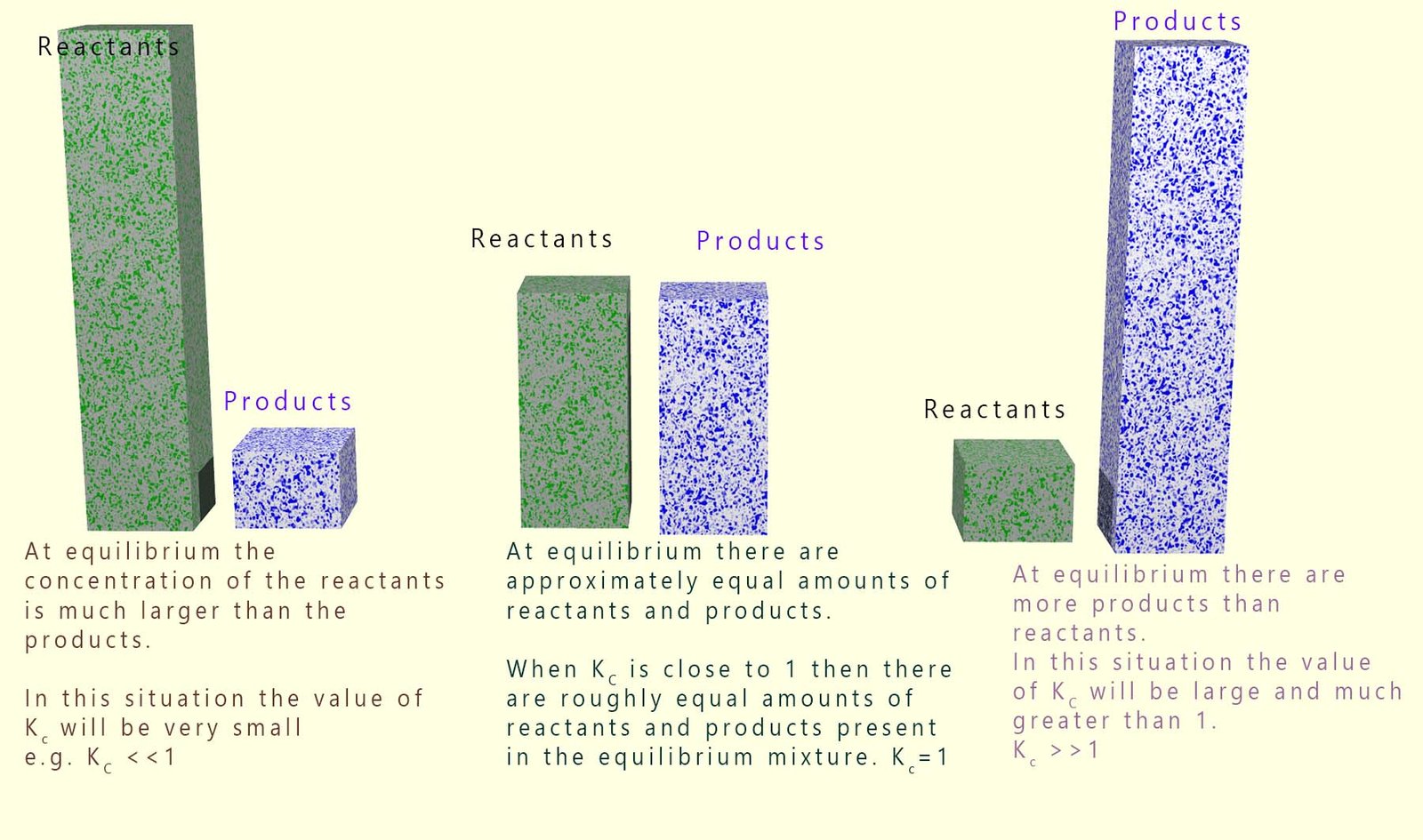
You can use Le Chatelier's principle to predict how the position of equilibrium will change when reaction conditions are altered (for example changing temperature, concentration or pressure). However for a given reaction the value of K_c changes only when the temperature changes.

For example consider what happens to the value of K_c when the temperature is changed. Remember that K_c is the ratio of [products]/[reactants] at equilibrium, so when the temperature is changed ask yourself what happens to the equilibrium concentrations of the reactants and products. From this you should be able to explain what happens to the value of K_c.

As an example consider the reaction shown below:

A_(aq) + B_(aq) ⇌ C_(aq)   ΔH = -ve

Here the forward reaction is exothermic; this means the reverse reaction is endothermic. So what would happen if this reaction was at equilibrium and we changed its temperature?

• If the temperature is increased then; according to Le Chatelier's principle the system will oppose the change. The position of equilibrium will shift to reduce the effect of the temperature increase, so it shifts in the endothermic direction (the reverse reaction). That means some product C is converted into reactants A and B so the value of K_c will decrease.
• If the temperature is reduced then the position of equilibrium shifts in the exothermic direction (the forward reaction). More reactants are converted into products; so the value of K_c will increase.

You should still be able to use Le Chatelier's Principle to explain what happens to the position of equilibrium when the concentration or pressure is changed, but at constant temperature these changes do not change the value of K_c. This is discussed in detail on the page which deals with Le Chatelier's principle.

Self-check: units of K_c

Have a go at these without writing out full expressions. Just decide what the final units of K_c will be.

Key Points

Practice questions

Check your understanding - Questions equilibrium constants.

Next