
Enthalpy changes involving solutions
A coffee cup calorimeter

Many reactions we study in chemistry take place in solution, for example neutralisation
of an acid using
an alkali is a chemical reaction that takes place in solution.
In this reaction the reactants and the products
are the system. The water and
the calorimeter are part of the surroundings. If the reactants undergo an
exothermic reaction then the
heat produced will heat the water
and as long as the calorimeter is well insulated
we can use the temperature change to calculate the
enthalpy change for the neutralisation reaction taking place here. A simple but
effective calorimeter is shown opposite.
Here a polystyrene coffee cup is used to hold the two solutions
that are reacting. Polystyrene is an excellent
insulator but this simple calorimeter can be improved if we simply
place the polystyrene cup inside another
cup to further insulate the reaction and prevent heat from leaving or
entering the solution. The cork lid
will also prevent heat loss by evaporation if the reaction is
exothermic and also prevent heat from the
surrounding entering the solution if the reaction is
endothermic.
Calculating enthalpy of neutralisation
Neutralisation reactions are exothermic.
When an acid and an alkali
react they form a salt and water.
Acid(aq) + alkali(aq) → salt(aq) + water(l)
A definition you should learn is:
The standard enthalpy of neutralisation is defined as:
The enthalpy change when an acid is neutralised
by an alkali or base to form one mole of water under standard conditions (298K, 100 kPa).
Consider the neutralisation reaction between the strong acid;
hydrochloric and the strong alkali sodium hydroxide. An equation for this neutralisation reaction is given below:
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)
Here the acid and alkali
react in a molar ratio of 1:1. We can use the simple coffee cup
calorimeter to measure the enthalpy of neutralisation here.
 Method.
Method.
- Rinse out a 25ml pipette using a dilute hydrochloric acid solution.
Clean a second pipette but this time rinse it out using a
dilute sodium hydroxide solution.
- Using the two clean pipettes measure out 25ml of 1M HCl and 25ml of 1M NaOH and place each of the solutions
in two separate expanded polystyrene cup. Each cup should be sitting
on a working magnetic stirrer.
- Using an accurate thermometer (one that measures to at least 0.10C) measure the temperature
of
each solution every minute for at least 5 minutes to ensure both
solutions are at room temperature.
Record the temperature of each solution in a table.
- Place the coffee cup containing 25ml of hydrochloric acid
into another coffee cup so that you have one
cup sitting inside another as shown in the diagram opposite. Put the calorimeter on top of a magnetic
stirrer and ensure the solution is being well stirred.
- Record the temperature of the acid in a table every 30 seconds for 4 minutes.
- On the fourth minute pour the 25ml of sodium hydroxide (NaOH) into the acid.
Do not record the temperature at the time
of mixing but start recording the temperature again at 5 minutes.
Continue to record
the temperature of the solution every minute for a further 10 minutes or until the temperature reaches room temperature.
Calculating the enthalpy of neutralisation
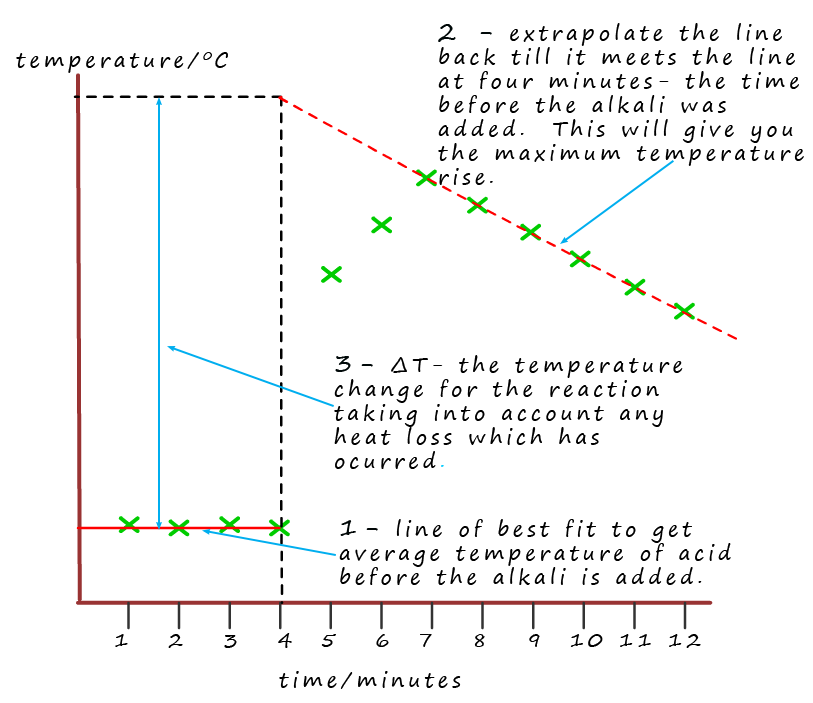
Neutralisation reactions are very exothermic reactions and can release large amounts of
heat energy. Here we
are also recording temperature changes over a fairly long period of time, ten minutes or so and
despite our best efforts
with insulation and using two polystyrene cups
some heat loss to the surrounding
will take place, especially if the
reaction is very exothermic and releases large amounts of heat energy.
However it is possible to compensate for SOME of this heat loss by using an extrapolation method as shown in the
graph opposite.
Here you can see a set of results obtained by a student, they have plotted their results on a graph
and extrapolated to find the maximum temperature reached to try and compensate for heat loss to the surroundings.
Example 1:
Let's use the example above to calculate the enthalpy of neutralisation when 25ml of 1M
hydrochloric acid
is neutralised by a 25ml of a 1M sodium hydroxide solution. Let's assume that the maximum temperature rise obtained from the graph in the example above was 70C.
- Total volume of the solution is 50ml. The mass
of the solution will be therefore be 50g since the density of water
is 1g/cm3
(1ml of water has a mass of 1g). We will assume that solution formed has the same density as water.
- The specific heat capacity of water
is 4.2 kJ kg-1K-1 or 4.2 J g-1K-1.
- Simply use the equation below to calculate the enthalpy change:
q = m x c x ΔT
Where:
- q = amount of heat energy taken in by the water (kJ).
- m = mass of water in kilograms (kg).
- c= specific heat capacity of water in kJkg-1K-1
- ΔT= change in temperature in degrees Kelvin, but since 1k = 10C then it can be in either without
any error in your calculations.
Substituting in the values we have:
q = m x c x ΔT
= 50 x 4.2 x 7
= 1470J or 1.47kJ
To calculate the molar enthalpy of neutralisation we simply need to scale up to work out the enthalpy change when 1 mole of water is formed. In the neutralisation equation above 1 mole of water is formed from 1 mole of acid, so if can work out the enthalpy change for 1 mole of acid and this will equate to the formation of 1 mole of water.
First calculate the number of moles of acid used in the experiment:
Moles of acid used = concentration of acid x volume
= 1 x 25/1000
= 0.025 mol
So 0.025 moles of acid gave a temperature rise of 70C. To scale this up to molar quantities simply divide the enthalpy change obtained from the experiment by the number of moles used to get the molar enthalpy of neutralisation:
ΔH = q/number of moles
=1.47kJ/0.025 mol
= -58.8 kJ mol-1
(The answer is negative since it is an exothermic reaction).
Example 2 - Displacement reactions.

Displacement reactions occur when a more reactive metal removes or
displaces a less reactive metal from a
compound or solution. Displacement reactions
can be very exothermic, especially if the
two metals involved are far apart in the reactivity series. For example zinc will displace copper
from a
copper sulfate solution according to the equation below|:
Zn(s + CuSO4(aq) → ZnSO4(aq) + Cu(s)
1mol 1mol 1mol 1mol
Example
The method used is very similar to that for the neutralisation reaction discussed above. 50 ml of 0.75M copper sulfate solution was pipetted into a
coffee cup
calorimeter and the temperature
was recorded every 30 seconds for 4 minutes. 5g of zinc powdered
was then added to the copper
sulfate solution and stirred continuously and the initial temperature was taken one minute later, the temperature was then recorded every 30 seconds until a maximum temperature
was
reached. Then the temperature was recorded for a further 5 minutes. The
initial temperature of the
solution was 24oC and the final temperature was 540C. This
reaction is
slow and the student obtained the final temperature by
extrapolation as in the previous example above.
| Moles of copper sulfate present |
Moles of zinc present |
Number of moles = concentration x volume
= 0.75 mol dm-3 x 50/1000
= 0.0375 mol
|
Number of moles = mass/Ar
=5g/65
= 0.077 mol
|
The zinc is in excess, which is what is required.
This will ensure that the reaction goes to
completion and all the copper sulfate will react. In order to calculate the
enthalpy change
for this displacement reaction we only take into account the mass of the solution
as this is what we are measuring the temperature of.
So enthalpy change is calculated from:
q = m x c x ΔT
= 50 x 4.2 x 30
= 6300J or 6.3kJ
To calculate the enthalpy change per mole of copper sulfate
we simply scale up and use the formula below:
ΔH = q/number of moles of copper sulfate
=6.3kJ/0.0375 mol
= -168kJmol-1
Key Points
- A simple coffee cup calorimeter can used to measure enthalpy changes for reactions
which take place in solutions.
- we use the equation below to calculate these enthalpy changes:
- q = m x c x ΔT
Here:
- q=the heat energy released or taken in by the system. This will obviously depend on whether the reaction is exothermic or endothermic.
- m= the mass of the substance, this is usually water. Recall that the density of water is 1g/cm3, this means that 1g of water has a volume of
1cm3 or 1ml.
- c= specific heat capacity. For reactions taking place in aqueous solutions the specific heat capacity of water is 4.18kJK-1kg-1. This simply means
that it takes 4.18kJ of heat energy to raise 1kg of water by 1 degree Kelvin or 1 degree Celsius.
- ΔT = This is simply the change in temperature that takes place during the reaction.
- The main source of error in the calorimeter is likely to be heat loss to the surroundings if the reaction is exothermic.
You should be able to describe how to use the extrapolation method discussed above to compensate for some of this heat loss.
Practice questions
Next



 Method.
Method.

