One of the big ideas in this part of the course is spotting the trends and patterns in the ionisation energies of elements across a period and down a group in the periodic table. But to really understand these patterns and trends; it helps to step back and first look at how the size of atoms and ions changes across a period and down a group. Measuring the size of an atom might sound simple, but as you’ll see; it’s not quite as straightforward as measuring its radius or diameter with a ruler!
You might already be asking: how can we talk about the size of atoms at all when they don’t have a neat outer edge? Electrons exist in orbitals, that is regions where there’s a high chance or probability of finding them, but these regions or orbitals fade out gradually rather than stopping suddenly, that is they have fuzzy edges. This makes it impossible to draw a sharp line around atoms.
Since we cannot measure the radius or diameter of an atom directly since it has no defined sharp edges or boundaries; we will instead define the atomic radius as half the distance between the two nuclei in identical atoms which are bonded to each other; when this measurement comes from a covalent bond this distance is often called the covalent radius of an atom; though A-level exam board prefer the term atomic radius rather than covalent radius e.g. in the diagram below there are two atoms labelled A. The atomic radius of atom A would be half the distance between the nuclei, so in this case the atomic radius of atom A would be 50pm (50 x 10-12m).
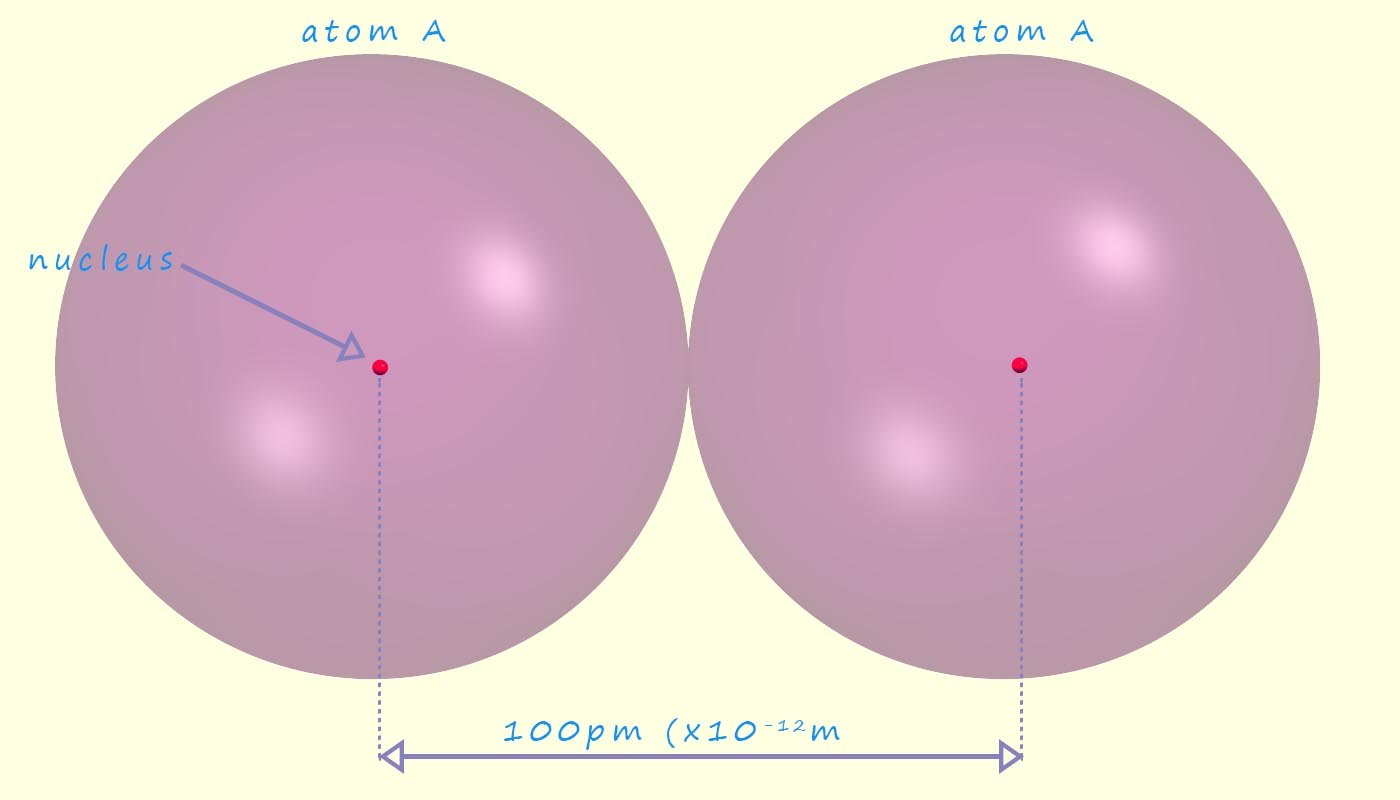
Measuring the distance between two nuclei in a solid is a common method used to find the atomic radius of an atom, especially for metals that form crystals with regularly arranged atoms. In this case, we often talk about the metallic radius, which is half the distance between neighbouring nuclei in a metallic lattice. We can use techniques like X-ray diffraction to measure these distances very precisely. The distance between these bonded nuclei is then divided by two to estimate the radius of a single atom (assuming a spherical shape for simplicity).
For non-metals, we can analyse molecules where the atoms are covalently bonded. The bond length; which is defined as the distance between the two nuclei of the bonded atoms in a covalent molecule while the covalent radius is defined as half the bond length. The bond length in a covalent molecule can be measured using spectroscopy techniques like microwave spectroscopy.
What trends might you expect to find in the atomic radius
of atoms if you were to go down a group in the periodic table? Or what about
the trends present as we cross a period in the periodic table?
Well take the alkali metals (Li, Na, K, Rb, Cs) in group I of the periodic table as an example; as we
descend group I an extra
electron shell or principal energy level is added for each element.
Li in period 2 has an electronic configuration
of 1s22s1,
Na in period 3,
has an electronic configuration of 1s22s22p63s1, now adding
the extra electron shell as we move down group 1 in the periodic table will increase the atomic radius or in this case the metallic radius of the metal atoms.
The next element in period 4 after sodium is potassium; now potassium will have an electron configuration of 1s22s22p63s23p64s1, its outer shell valence
electron is in a 4s sub-shell,
so it will be even larger than sodium. The table below lists the atomic radius for each of the alkali metals up to rubidium and the trend in the atomic radius is as mentioned above; as you descend a group in the periodic table the atoms get larger.
| element | Li | Na | K | Rb |
|---|---|---|---|---|
| atomic radius (pm) | 128 | 166 | 203 | 290 |
| relative sizes of atoms |  |
|
|
|
Moving down any one particular group in the periodic table to the next period adds an additional electron shell which increases the size of the atom. This is despite the fact that the nuclear charge; that is the number of protons present in the nucleus is increasing as we descend the group; which will have the effect of trying to pull in the electrons and decrease the size of the atom, however as the atoms get larger there will be an increase in shielding which will help screen the additional nuclear charge. That is the shielding helps to reduce the effective nuclear charge experienced by the outer valence electrons, mitigating some of the inward pull or attraction towards the nucleus; this is explained in more detail below. So overall the increase in the number of electron shells has a greater influence on the atomic radius compared to the increase in nuclear charge within a group.
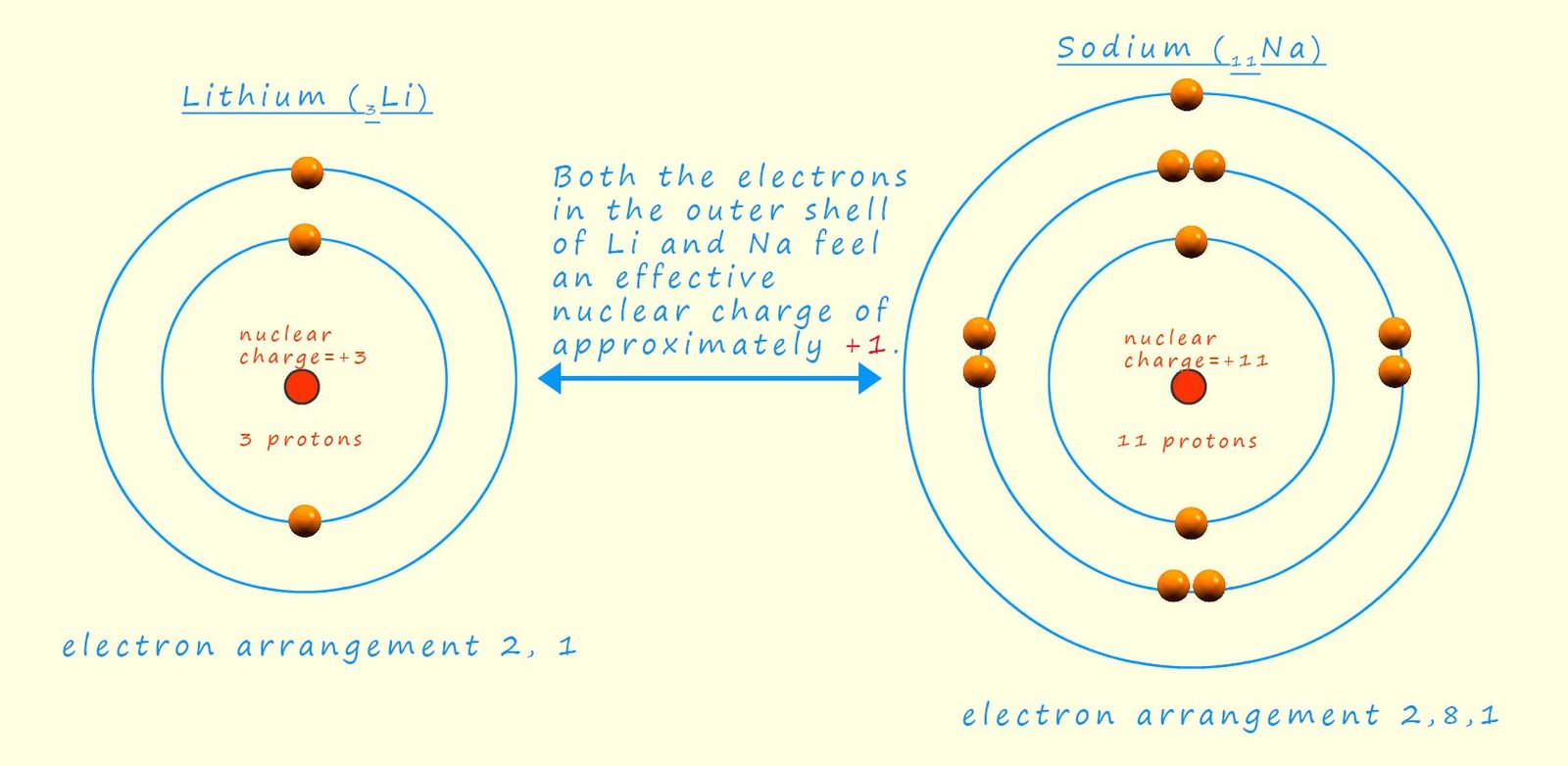
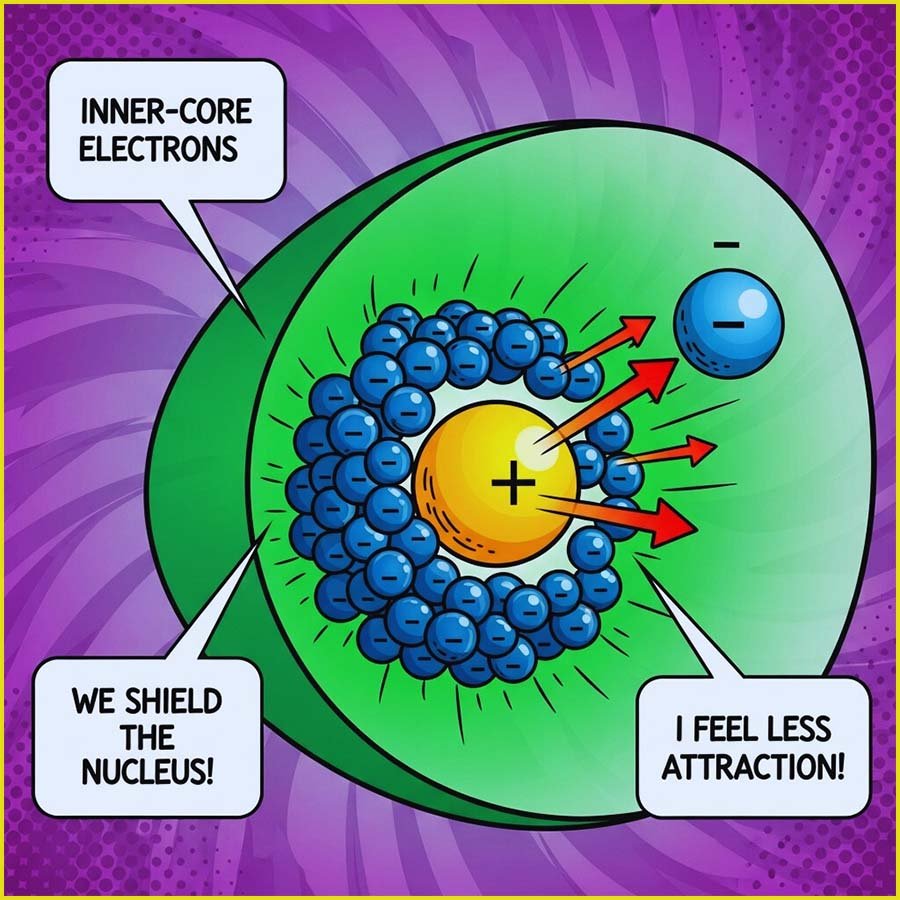To give a simple overview of electron shielding, consider lithium and sodium, alkali metals in group 1 of the periodic table. Lithium has an electron configuration of 1s²2s¹ and has 3 protons in its nucleus. While all the electrons in the lithium atom experience attraction from the positively charged protons, the two inner (1s) electrons are closer to the nucleus compared to the outer (2s) electron. This proximity allows the inner electrons to partially shield the outer electron from the full positive charge of the nucleus. We express this shielding effect as the concept of effective nuclear charge (Zeff). In this case, the Zeff experienced by the valence electron (2s) in lithium will be less than +3 due to the shielding by the inner electrons.
Similarly sodium (1s²2s²2p⁶3s¹) has 11 electrons. The inner or core 10 electrons (in the 1s and 2s/2p sub-levels) shield the outermost (3s) electron to a greater extent than in lithium because there are more electrons between the nucleus and the valence electron. The increased distance of the valence electron from the nucleus in sodium also weakens the attraction, further contributing to its lower overall attraction to the nucleus. If you would like to have a go at calculating Zeff values a quick search of "Slater values" will set you the right track, however these values are not required in A-level chemistry and a more simplistic approach can be found here.
The image below gives a representation of sodium and lithium atoms that you may have seen in your GCSE science course. We can obtain a rough estimate of the shielding present and the effective nuclear charge (Zeff) that the outer valence electron(s) feels by simply subtracting the number of shielding core electrons from the total number of electrons present. So in the case of lithium we have 2 inner core electrons and 3 electrons in total, so the Zeff is simply +1; while in sodium there are 10 inner core or shielding electrons and 11 electrons in total; so once again the effective nuclear charge that the outer valence electron feels is simply +1. However this electron is much further away from the nucleus than in the smaller lithium atom.
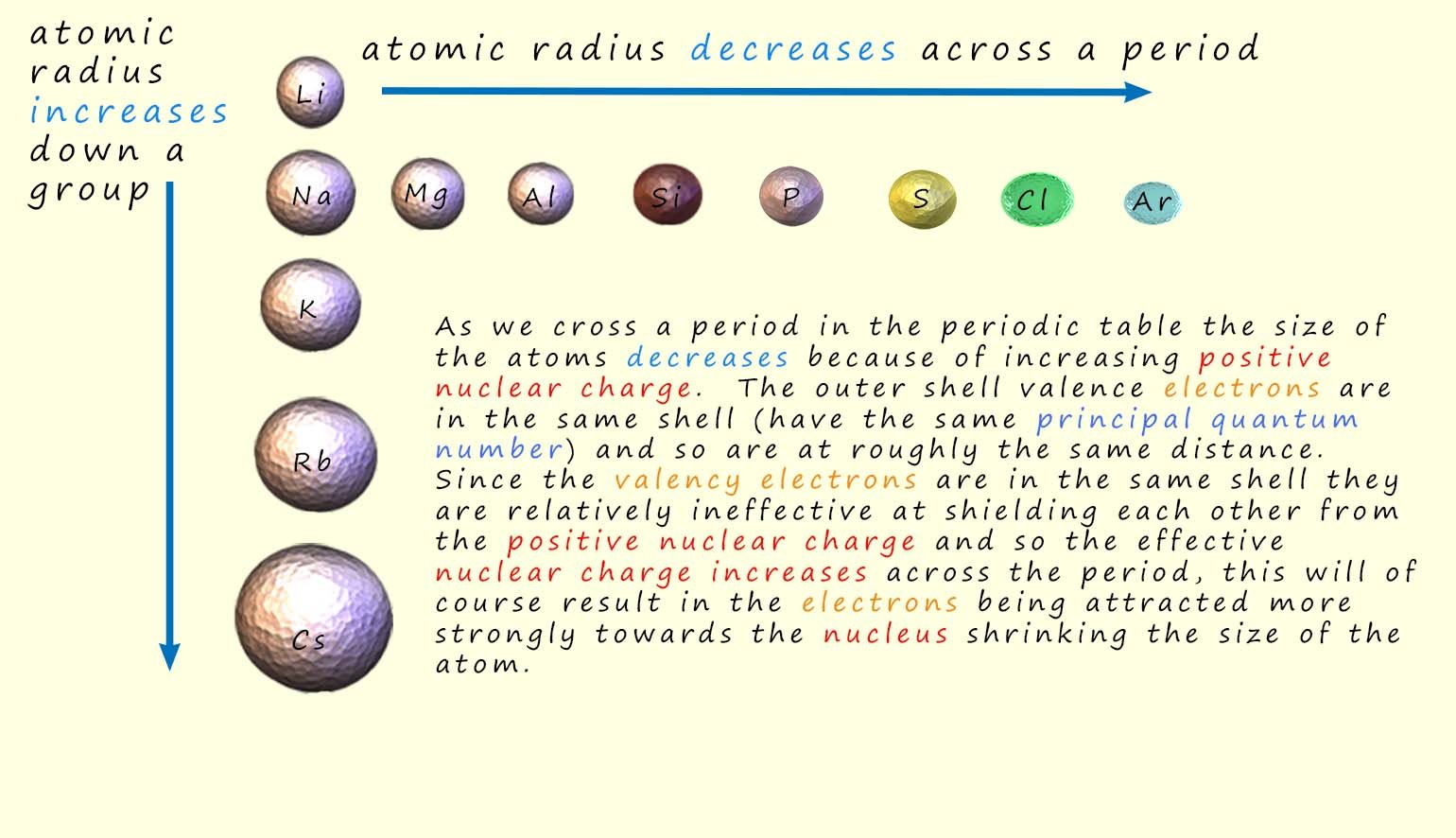
The atoms get smaller as we cross a period in the periodic table; this is perhaps not what you were expecting. However if you consider the electronic configurations of the elements and the increasing nuclear charge as we cross a period it is an entirely obvious conclusion. The decrease in the size of the atoms is simply because the outer shell valence electrons are all roughly at the same distance from the nucleus since they are in the same principal energy level/sub-level and the ability of electrons to shield each other from the effect of the nuclear charge is reduce by the fact that the valence electrons are all in the same principal energy level. The amount of shielding experienced by an electron depends both on the shell and sub-shell it is in. Generally valance shell electrons are:
In crossing period 3 the electrons are
being added to the 3s and 3p sub-shells
they are ineffective at shielding each other from the increasing nuclear charge.
So the effective
nuclear charge (Zeff) that each electron experiences is increasing
so the atoms decrease in size as a result.
This is illustrated in the diagram below:
Click a Trend / Observation (left), then click the matching Reason (right). Click a matched item to unmatch it.