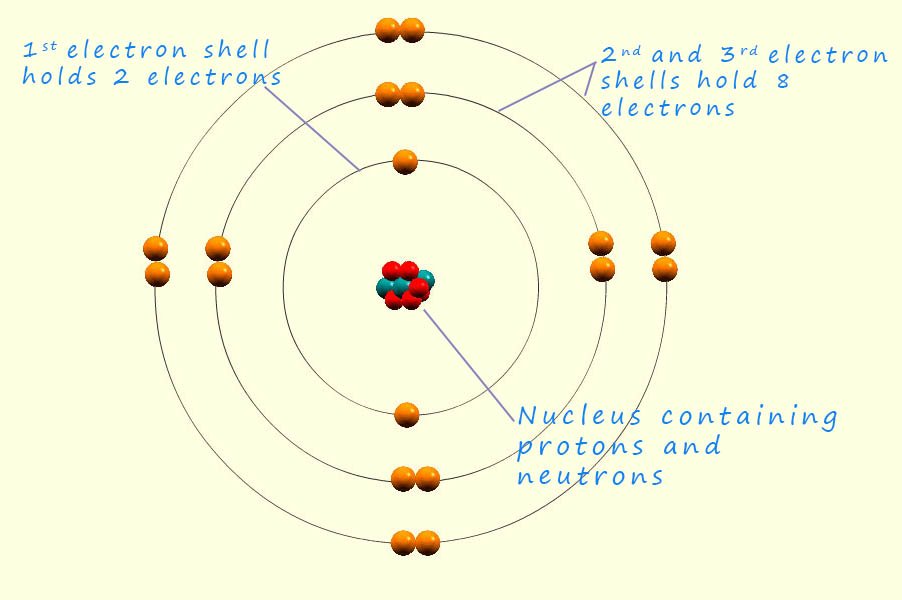
The model of the atom you are probably most familiar with is based mainly on the work of Ernest Rutherford and Niels Bohr. In 1911 the model of the atom which existed was based on Rutherford's nuclear model of the atom. Ernest had just discovered the nucleus following his now famous "gold foil experiment" but Rutherford's model of the atom; which replaced J.J. Thomson's plum pudding model said very little about how the electrons were arranged inside the atom. Rutherford's nuclear model of the atom established a very small dense nucleus at the centre of the atom but it lacked detailed specifics about the electron orbits within the atom. The electrons, with their negative charge were simply described as orbiting the nucleus in circular orbits at a distance. Although this was a major shift from the prevailing model at the time; Thomson's plum pudding model which had described the electrons as being simply embedded in a sphere of positive charge. Rutherford new nuclear model of the atom didn't define:
However in 1913 Niels Bohr; a Nobel prize winning scientist suggested that the electrons within atoms orbit the nucleus in circular or elliptical orbits and these orbits have fixed or discrete energy levels. Bohr used the new ideas which were developing in the field of quantum mechanics to successfully explain the lines present in the emission spectrum of a hydrogen atom.
However as much as Bohr's idea of fixed and discrete energy levels within atoms was a significant development in understanding the internal structure of the atom it had a few serious limitations, not least of which was it was unable to adequately explain the more complex emission spectra produced by atoms with more than one electron. The interactions of these additional electrons with each other and the nucleus were much more complex than that found in a simple hydrogen atom with its one electron and one proton, it was became increasingly clear that Bohr's model was a simplification of the actual internal structure of the atom and that the simple circular orbits assigned to the electrons did not accurately represent the behaviour of these electrons within atoms.
What was needed was a new theory to describe how the electrons were actually arranged inside the atom and this was provided in 1926 by the Austrian scientist Erwin Schrödinger who developed a new quantum mechanical model to describe the behaviour of the electrons within atoms.
Now Bohr was able to calculate the energies of the electron shells and proposed that electrons occupy specific allowed energy levels inside the atom. While Bohr's model offered a basic explanation for the electron arrangements within atoms and successfully explained the hydrogen atom's emission spectrum, it couldn't fully explain the complexities observed in emission spectrum for atoms with more than one electron.
To address these limitations, Erwin Schrödinger, an Austrian Nobel prize winning physicist introduced the quantum mechanical model of the atom in 1926. This model incorporates the concept of wave-particle duality, which we encountered when discussing the nature light and emission spectra. Wave-particle duality simply suggests that electrons or indeed any particle can exhibit both wave-like and particle-like behaviour. In the quantum mechanical model, the concept of fixed circular paths or orbits for the electrons around the nucleus in the atom as suggested by Bohr, is replaced by a series of mathematical equations called wave functions or orbitals. These wave functions define the energy and the probability of finding the electrons in a specific volume of space surrounding the nucleus.
This new approach proved more accurate model for describing the behaviour of electrons in multi-electron atoms than that proposed by Bohr and it also could accounted for the complexities observed in the atomic spectra of multi-electron atoms.
The solutions of the Schrödinger mathematical equations, known as wave functions, provide us with a set of quantum numbers. These quantum numbers describe the location, energy, and orientation in space of the electrons within an atom. One of these, the principal quantum number (n) is analogous to Bohr's principal energy levels.
| Principal energy level | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| type of sub-level found | s | s, p | s, p, d | s, p, d, f |
The image below shows a rather simplified picture of how the first three energy levels are split into various sub-levels. The image shows that:
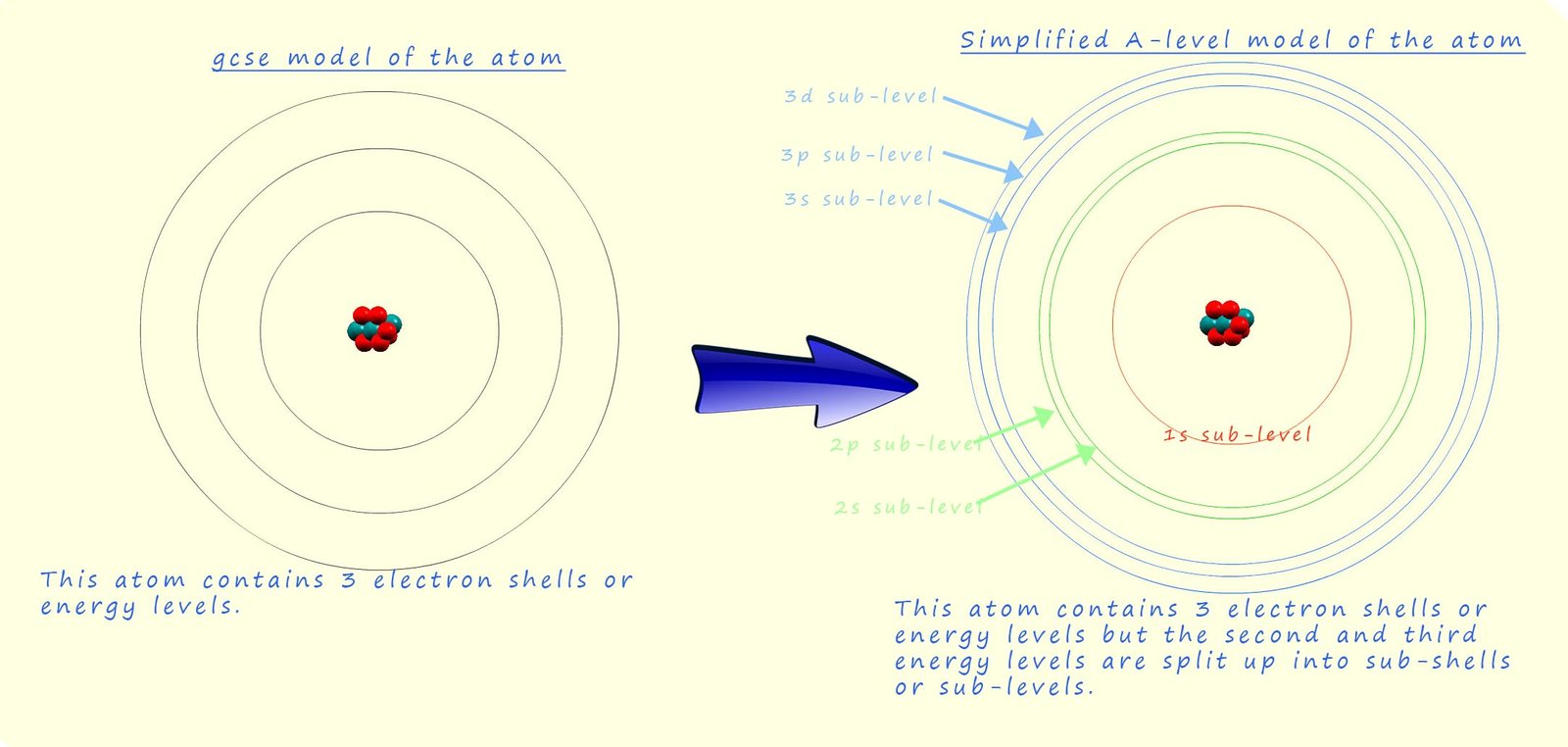
Each sub-level consists of orbitals, now orbitals are a region of space centre around the nucleus where there is a high probability (90% chance) of finding the electrons. Each individual orbital can hold a maximum of 2 electrons with opposite spins, now the number of orbitals increases as the principal quantum number increases, this means that the number of electrons that each electron shell can hold increases as the shells become larger. We can use the formula 2n2 to calculate the number of electrons present in each shell (n is simply the shell number or principal quantum number). This is summarised in the table below:
| First shell/energy level | Second shell/energy level | Third shell/energy level | Fourth shell/energy level | |
|---|---|---|---|---|
| sub-shells present | s | s, p | s, p, d | s, p, d, f |
| Number of orbitals present | 1 | 1, 3 | 1, 3, 5 | 1, 3, 5, 7 |
| Maximum number of electrons present in each sub-level | 2 | 2, 6 | 2, 6, 10 | 2, 6, 10, 14 |
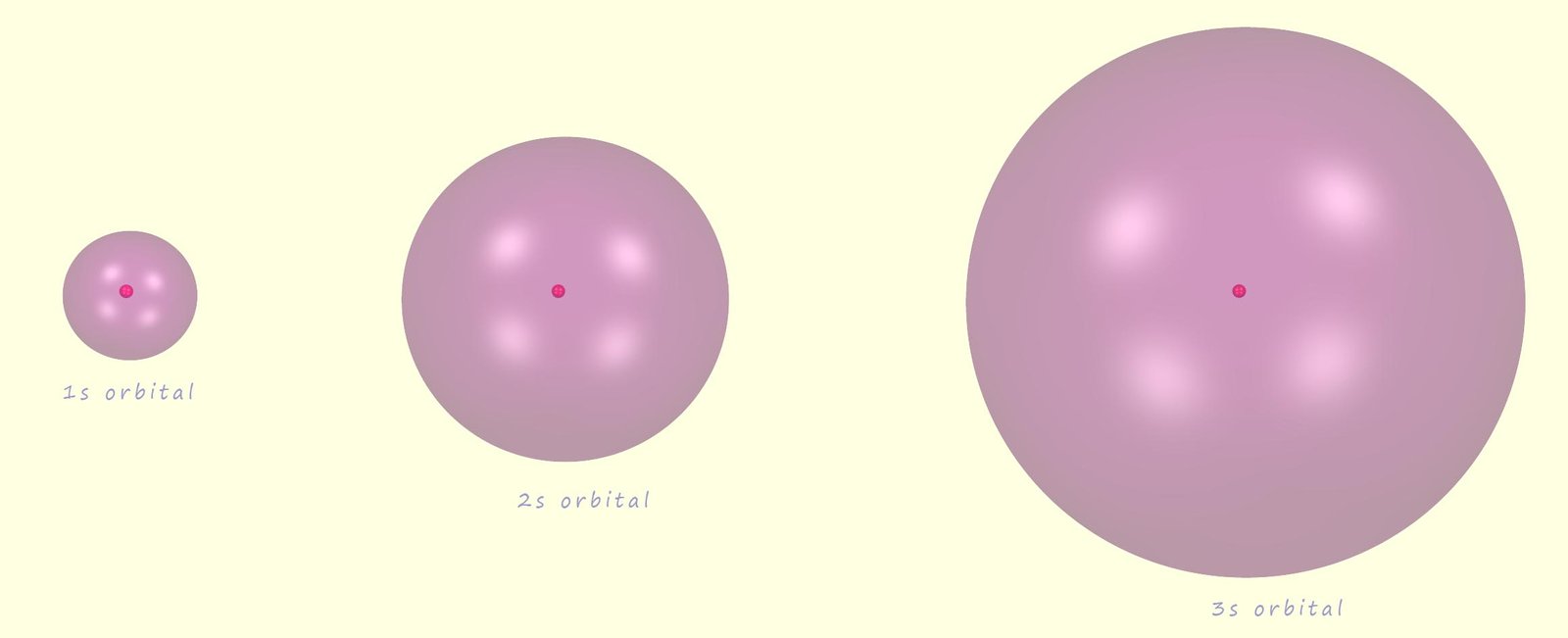
There are four types of orbital that we need to know about; these are s, p, d and f orbitals. Let's start with the lowest energy level in the atom, that is the 1s sub-level. Now there are 2 electrons in this sub-level and they are found in a 1s orbital. Now all s orbitals are spherical and centred around the nucleus; the image below shows the 1s, the 2s and the 3s orbitals which would be found in the first, second and third electron shells or energy levels; as you can see they are all spherical but differ only in size. the 2s and 3s orbitals although much larger than the 1s orbital but as with any orbital no matter its size they still only hold a maximum of 2 electrons (note the nucleus shown in the centre of each s orbital is not to scale and is shown much larger than it actually is).
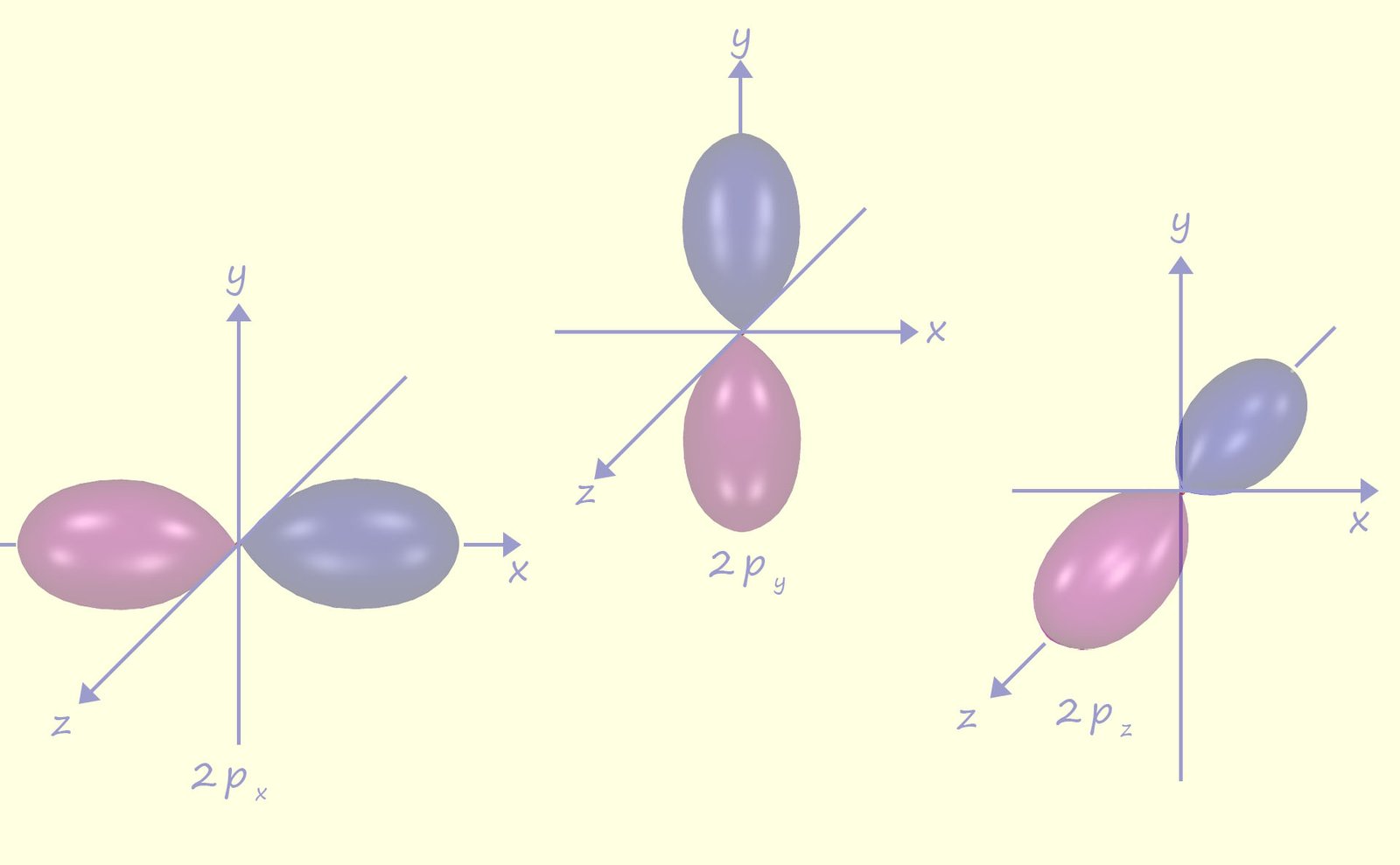
There are three p orbitals and each one is dumbbell shaped, one of the p-orbitals; named px lies over the x-axes, another named py lies along the y-axes and the last one name pz lies along the z-axes. The p orbitals are first appear in the second electron shell or energy level and so these three p orbitals are named 2px, 2py and 2pz. Now each p orbital can hold a maximum of 2 electrons and since there are three p orbitals then in total the p orbitals can hold a maximum of 6 electrons. The second energy level or shell also has a 2s orbital and three p orbitals so the second energy level can hold a maximum of 8 electrons in total.
The third principal shell (n = 3) can hold one 3s orbital, three 3p orbitals, and five 3d orbitals; so in total the third energy level can hold a maximum of 18 electrons. These five d orbitals have unique shapes with lobes oriented between specific axes. For example, the dxy orbital has lobes along both the x and y axes. Three of the five 3d orbitals have a clover leaf shape with the lobes of the orbitals in between the axes, for example the dxy orbital has its lobes between the x and y axes, while the dyz orbital has its lobes between the y and z axes. These three d orbitals are shown in the first image below:
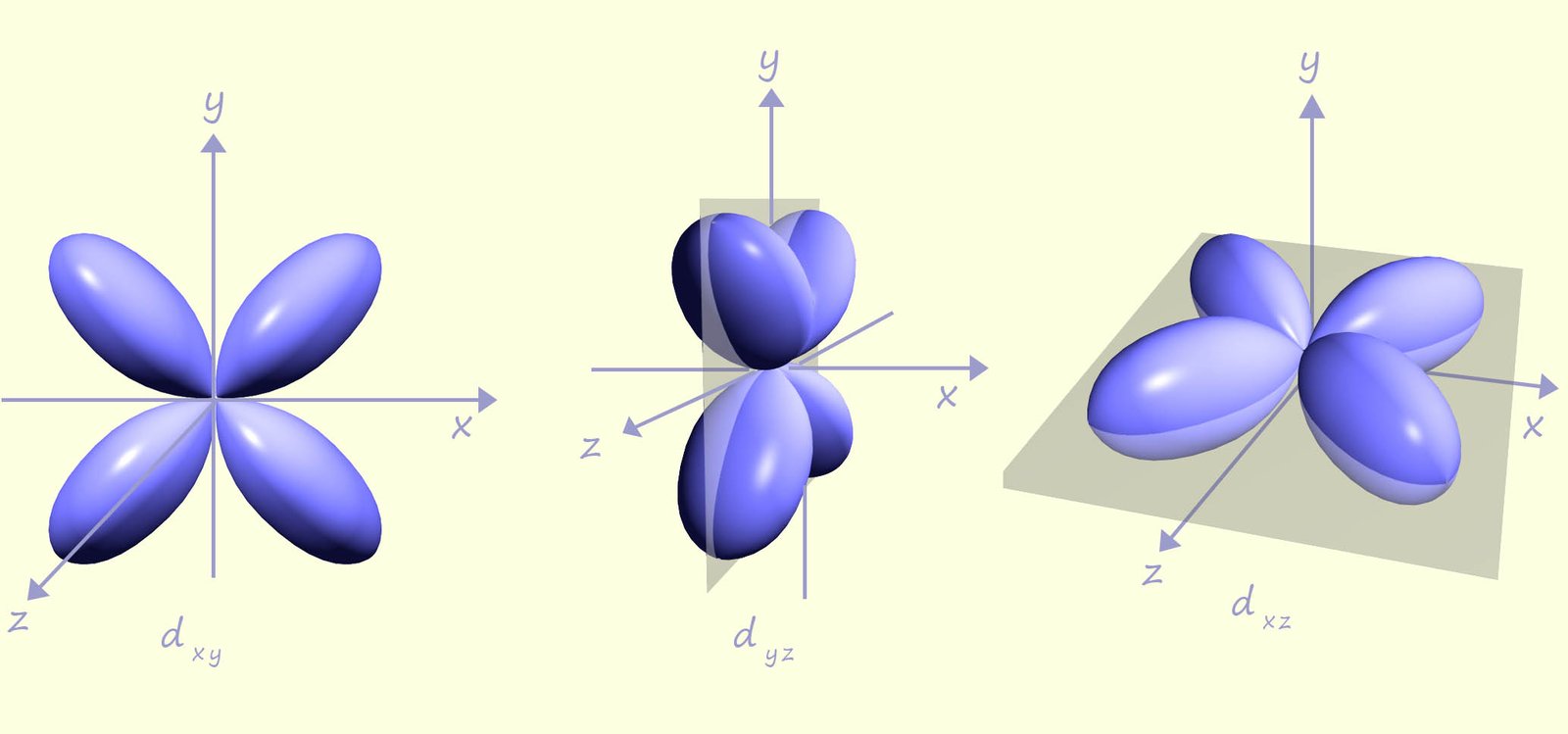
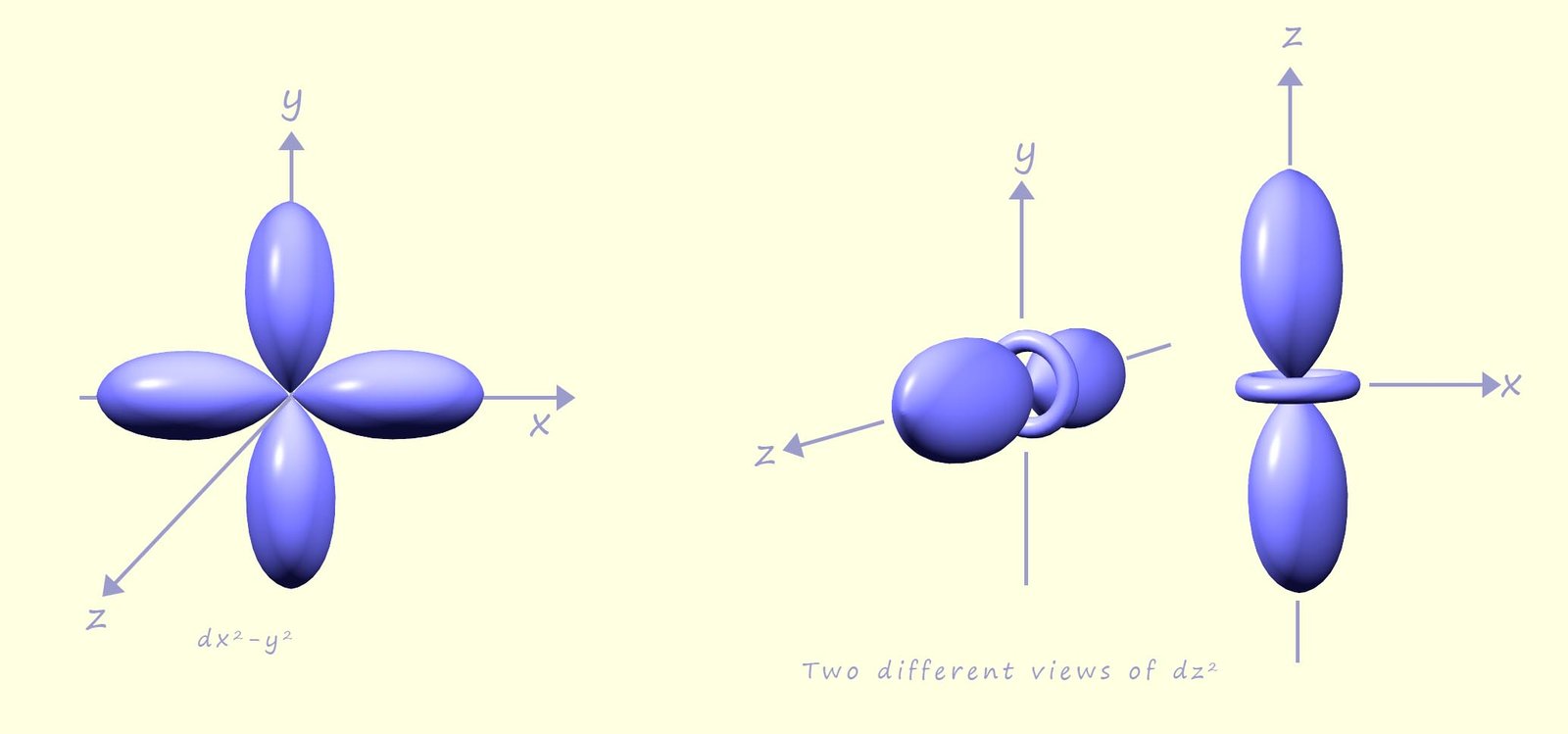
The image below shows the shapes of the last two d orbitals the dx2-y2 and the dz2 orbitals. The dx2-y2 orbital like the three d orbitals shown above is clover leaf shaped but unlike the d orbitals above its four lobes lie along the x and y axes and not in between. The last d orbital, the dz2 orbital has a completely different shape to the other d orbitals, it looks like a pz orbital with a donut shaped area of electron density around the centre. The image below shows 2 different views of the 3dz2 orbital. Since there are five d orbitals and each orbital can hols up to 2 electrons then in total the d orbitals can hold a maximum of 10 electrons. In the third energy level there will be 3s, 3p and 3d orbitals so the third energy level can hold a maximum of 18 electrons.
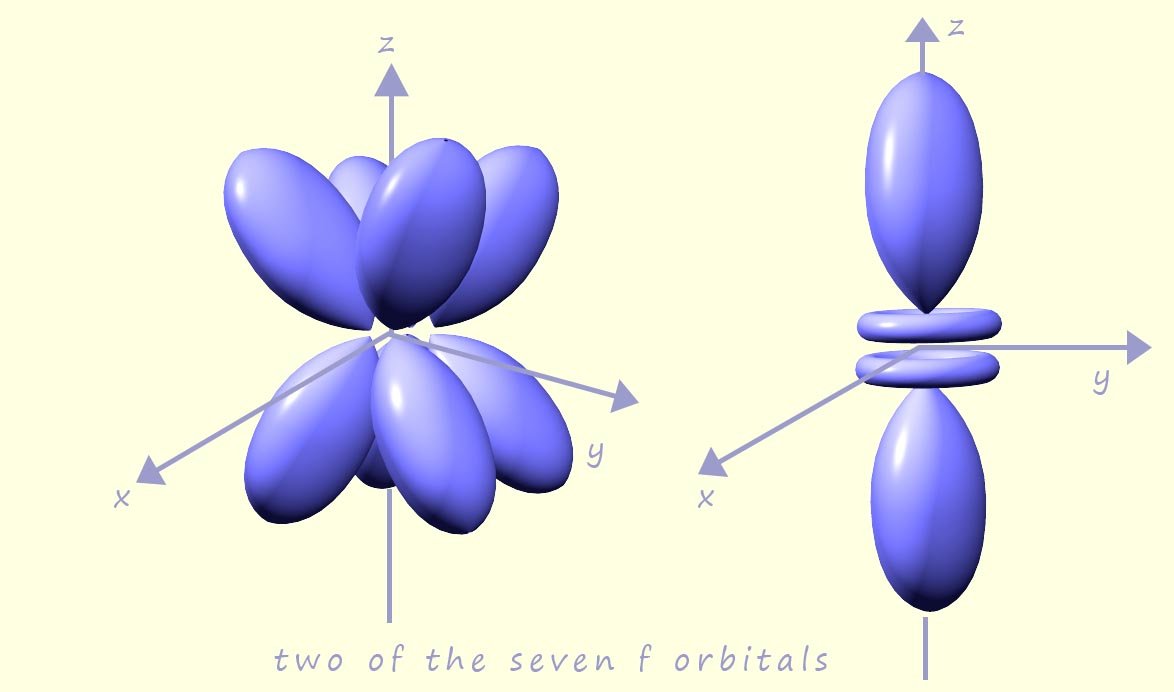
There are seven f orbitals, which first appear in the fourth electron shell or energy level; two of which are shown in the image opposite. This means that the seven f orbitals can hold a maximum of 14 electrons. However it is very unlikely that you will need to consider these orbitals in your A-level chemistry course so if you wish to find more about these orbitals and their properties then a quick internet search will no doubt yield some promising and interesting results.