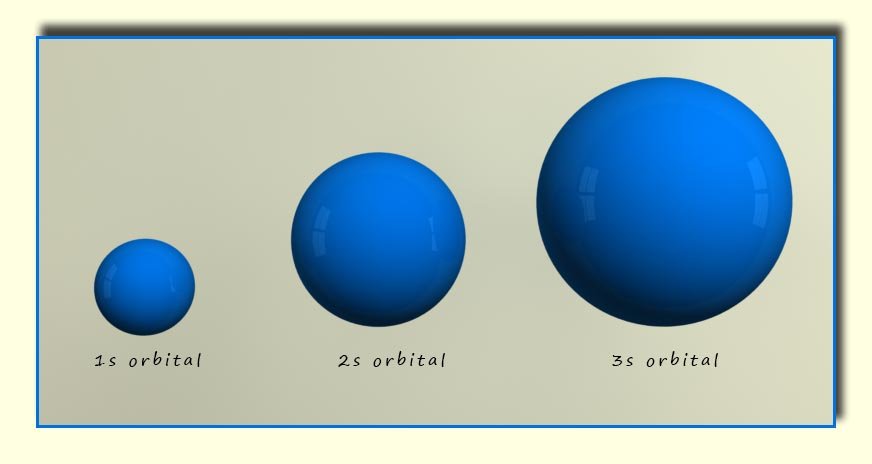
The s-orbitals are spherical in shape. They all have a value of 0 for the azimuthal or angular momentum quantum number(l). The main
difference between the s-orbitals found
in different shells is the size, as shown in the diagram below.
It is easy to imagine the nucleus at the centre of the s-orbital with the electron density spread throughout the orbital.
There are 3 p-orbitals and they all have a dumb-bell like shape as shown below, but they are arranged differently in 3d space:
The electron density in the p-orbitals is concentrated in two lobes on either side of the nucleus. There are 3 p-orbitals; they are identical in size and shape but are simply arranged differently along each of the x, y and z-axes in 3d-space. The three p-orbitals are called Px, Py and Px, the labels simply indicate the axis along which the lobes of the p-orbital are located. The first p-orbitals are found in the second shell; the p-orbitals in the next shells are similar in shape and orientation but are simply larger. Each p-orbital can hold 2 electrons, meaning that the 3 p-orbitals hold 6 electrons in total if they are full.
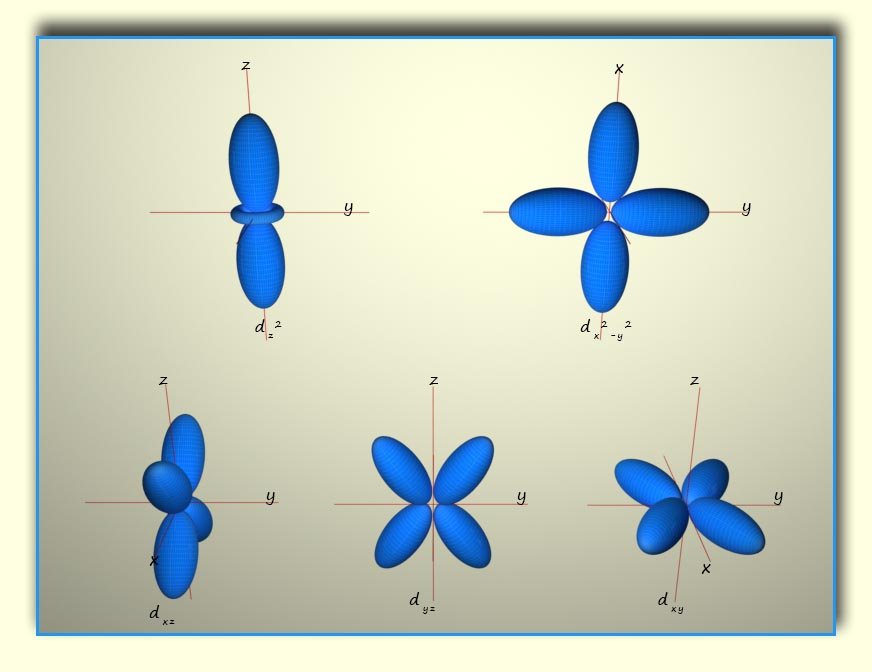
There are 5 d-orbitals. Three of them have lobes orientated between the axes, for example the dxz orbitals has its lobes orientated between the x and z axes. Two of the orbitals are arranged differently, the dx2-y2 orbital has its lobes orientated along the x and y axes while the dz2 orbital resembles a p-orbital with its 2 lobes but it has a doughnut like ring of electron density around its centre. The shapes of the d-orbitals is shown in the image below:
The orbitals in each principal energy level in hydrogen and other one electron atoms such as He+ as we
have seen are degenerate (same energy) but in multi-electron atoms the sub- shells or sub-levels and hence
the orbitals in each principal energy level are no longer degenerate, for example the 3s, 3p and 3d sub-shells
in hydrogen are all degenerate but in multi-electron atoms the repulsion between the electrons leads to a
splitting in the energy levels, for example the 2s sub-shell is lower in energy than the 2p sub-shell. The
reason for the splitting in the energy levels is due to the repulsion between the electrons and also the
effective nuclear charge that each electron feels.
In atoms with many electrons we need to consider how each of the electrons interact with each other in
terms of repulsions and also the attractive forces that each electron will experience from the positively
charged nucleus. This is no easy task and it is much simpler to just consider a model where we consider
each electron individually and try to estimate the forces it is experiencing. Any electrons between the
nucleus and the electron we are considering will effective screen or reduce the size of the attractive forces
it experiences from the nucleus. This net charge that an electron experiences is called the effective
nuclear charge, it is simply the number of protons in the nucleus minus the average number of electrons
between it and the nucleus. This means that electrons in the outer shells will feel a much smaller
force of attraction from the nucleus because the inner shell electrons will screen or shield them
from the positive charge in the nucleus. The effective force that each electron feels will depend
also on the shapes orbitals as this will clearly have an effect on how well the nucleus is shielded
or screened, for example an electron in an s-orbital is more likely to closer to the nucleus than an
electron in a p-orbital, this means it will experience a large attraction from the nucleus and will be
pulled in closer to the nucleus, so it will be lower in energy than the p-orbital electrons. This
leads to a diagram similar to the one below which shows the relatives energies of the sub-shells in
a hydrogen atom compared to those in multi-electron atoms: