Note: Some of the content below is a little above the requirements for A-level chemistry and is NOT included in the specification but I think you might find it helpful and useful, especially since it tries to give some historical information and a brief introduction to some of the many scientists who contributed to our current understanding of the structure of atoms.

A brief history of the atom

In the early 1900s the accepted model of the atom was based on J.J. Thomson's plum pudding model. This model of the atom thought of the electrons as tiny particles, much like super small billiard balls embedded within a positively charged 'pudding'. However in 1911 Ernest Rutherford's proposed his nuclear model of the atom which replaced Thomson's plum pudding model. Rutherford's atomic model was based on his famous gold-foil experiment which described the atom as having a tiny, positively charged nucleus at its centre with the electrons orbiting the nucleus in circular orbits.

However Rutherford's model of the atom was replaced in 1913 by the atomic model developed by the Danish physicist Niels Bohr. Bohr built upon Rutherford's atomic model by introducing quantised energy levels for the electrons, meaning the electrons could only occupy certain specific allowed energy levels. These allowed energy levels were simply the electron shells or orbits" around the nucleus, this differed from Rutherford's model where the electrons would be free to orbit the nucleus in any energy level or shell as long as it was a stable orbit.

However it's important to note that while the nuclear model proposed by Rutherford and later refined by Bohr was the accepted model at the time, scientists were already starting to grapple with the limitations of this new model in explaining observations and results many experiments; for example one such limitation of Bohr's model of the atom was its inability to fully explain the observed patterns in the absorption and emission spectra of atoms with more than one electron. These limitations encouraged many scientists to develop new ideas and theories on the structure of atoms, leading to the development of a new theory called quantum mechanics, in this new quantum model the atom still had a nucleus at the centre but it was proposed that the electrons are not found in fixed orbits around the nucleus, but rather they exist in clouds or orbitals, which are a 3d volume in space centred about the nucleus where there is a high probability of finding the electrons. This new quantum theory also included the idea of wave-particle duality for the electron.

Wave-particle duality

Before we carry on with the discussion on the structure of atoms let's look at another issue that was causing some confusion in the scientific world for many centuries, what is the nature of light? That is does light consist of a wave or a particle? The nature of light is one of the weirder things in science! It doesn't quite fit into our everyday understanding of the world and the objects we see in it. Light exhibits both wave-like and particle-like behaviour or characteristics, that is it exhibits wave-particle duality

Isaac Newton proposed that light consisted of a stream of particles; his theory was outlined in his book Opticks published in 1704. However many other scientists including many well known and respected scientists such as Christiaan Huygens strongly supported the wave nature of light.

Further experiments in the early 1800's by scientists such as Thomas Young and Augustin Fresnel's suggested that light did indeed have wave like properties; for example:

• Young's Double-Slit Experiment (1803): One piece of evidence which strongly suggests the wave nature of light is that it forms an interference pattern when it passes through two narrow slits which are very close together. To explain what an interference pattern is imagine tossing two pebbles into a pond. When these two pebbles hit the water surface at the same time and fairly close together, they create a pattern of circular ripples that can strengthen or cancel each other out, depending on how they meet, this is shown opposite.

The double-slit experiment with light works kind of like this. When light is shone through two slit which are close together, just like the pebbles on the water surface. Now if light behaved only like tiny particles, then we would expect to see two bright stripes where the light hits a screen behind the slits. However this is NOT what is observed, because light also has wave like characteristics, the waves travelling through each slit spread out in a similar way to the water ripples produced when the two pebbles hit the surface of the water. When these spreading light waves pass through the two slits, they can overlap. Where the peaks of the light waves line up they build upon each other and they create a bright spot (like two ripples strengthening each other) and where a peak meets a trough (think high point meeting a low point), they cancel each other out creating a dark spot on the screen. This creates a pattern of alternating bright and dark bands on the screen – an interference pattern. This pattern wouldn't happen if light consisted of particles – it shows light waves interacting with each other. So, the double-slit experiment is strong evidence that light has a wave nature.


• Fresnel's Diffraction: This experiment demonstrated the diffraction of light, now diffraction is when waves bend around corners or pass through small openings; as shown in the diagram below, for example when water waves hit a rock in the middle of a pond instead of stopping completely at the rock, the waves will gently bend around it and continue spreading outward in circles or when waves at sea enter a narrow harbour they appear to spread out as they enter the narrow harbour opening. Now when light waves encounter an edge or obstacle just like water waves they bend slightly around it, this means that areas you might expect to be in shadow are in fact lit. This bending effect is another key property of waves. Fresnel's work with diffraction helped confirm that light can behaves like a wave, not just a stream of particles.

Wave-particle duality- the two faces of light

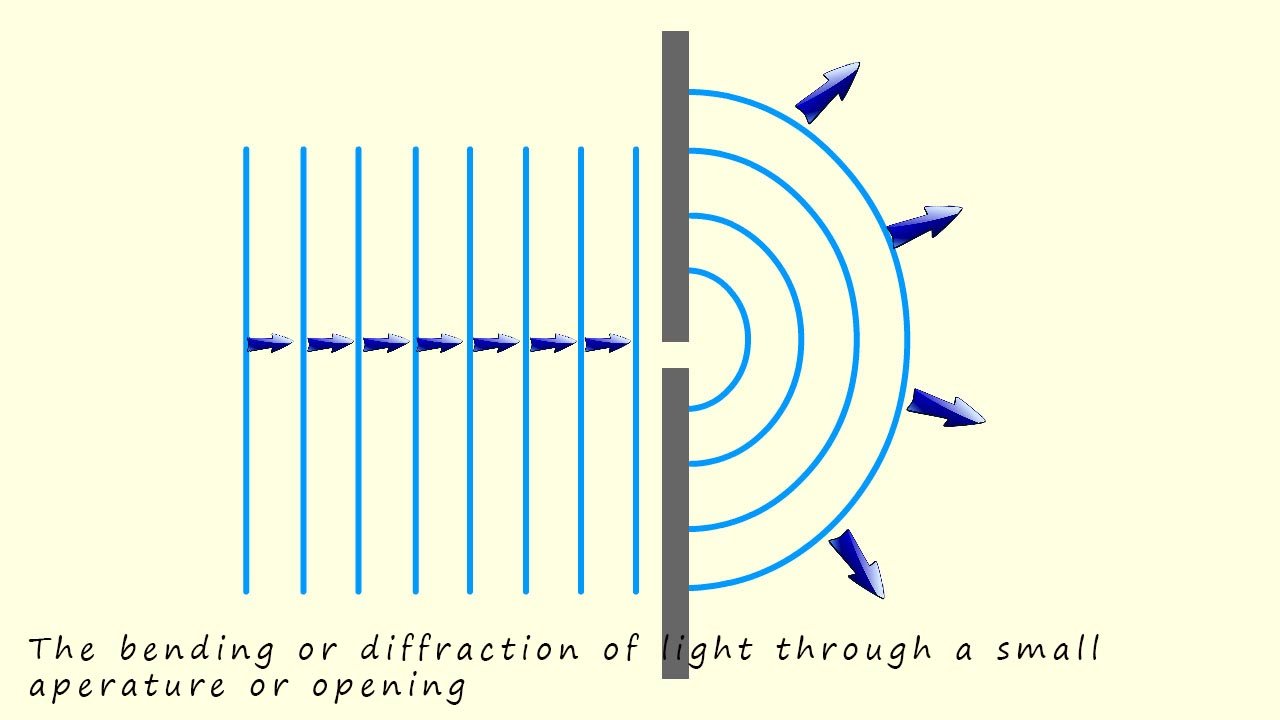
So while Isaac Newton proposed that light consisted of a stream of particles, experiments by Thomas Young and Augustin Fresnel in the early 1800s demonstrated diffraction and interference patterns, supporting the wave nature of light." While in 1905 Albert Einstein extended Max Planck's quantum theory to explain how light could knock electrons out of metal surface. Unlike the prevailing wave theory of light, Einstein proposed that:

• Light consists of discrete packets or particles of energy called photons.

and that:


• The energy of a photon is directly proportional to its frequency, as described by Planck's equation (E = hf, where E is energy, h is Planck's constant, and f is frequency).

According to Einstein when a photon collides with an electron in a metal, it transfers its entire energy to the electron. If the photon's energy (determined by its frequency) is greater than the work function of the metal, that is the energy required to remove an electron, then the electron will be ejected from the surface of the metal.

This idea of wave-particle duality might seem a bit weird and indeed it is, in the normal world, things are either particles (like pebbles) or waves (like ripples in water but in the world of atoms, light and sub-atomic particles like electrons it appears that they can behave or they have the characteristics of both! To be honest scientists don't fully understand why yet, but it's one of the strange and fascinating things about how light, atoms and sub-atomic particles behave and is one of the features of quantum theory, a theory which tries to explain and describe how light, atoms and the "stuff" that makes them up behaves.

Max Planck and quantised energy

Although Einstein used the idea of energy being delivered in small packets or quanta to explain the photoelectric effect, these small packets of energy or quanta were later referred to as photons, now this idea of energy being available in discrete packets was initially developed by Max Planck. Planck introduced this revolutionary idea that energy is quantised, meaning it comes in discrete packets rather than in a continuous flow.

Around 1900 Planck had been working on a problem that had baffled many scientist for a long time, this problem was to try and find a link between the wavelength, temperature and the intensity of light emitted by hot objects. Now hot objects obviously emit light and the intensity and colour of this emitted light changes with temperature, for example imagine a metal poker in a fire. As the poker heats up, it starts to glow, the hotter it gets, the brighter it glows and the colour and intensity of the glow changes from longer wavelengths orange and red light which is emitted at low temperatures to shorter wavelength but more intense blue and blue-white light as its temperature rises. Existing theories predicted that hotter objects should emit more and more light at all wavelengths but this wasn't what was observed and this was proving a difficult problem to solve.

However in 1900, Planck proposed a solution to this problem by introducing the concept of quantised energy. He suggested that the energy emitted by hot objects is not continuous as had been expected but instead comes in discrete amounts or packets of energy which he called quanta. This idea was revolutionary and initially not well received in the scientific community; however this revolutionary new idea marked the birth of quantum theory. Planck's constant (h) emerged from this work and his now famous equation E=hν (where E is energy and ν is frequency) showed that energy is proportional to frequency. (Note I have used two different symbols frequency on this page, that is f and ν, you will no doubt find that this is the case depending on which course and textbook you are using!)

Matter waves

E=mc²

This famous equation shows the equivalence of mass (m) and energy (E). It essentially states that mass and energy are different forms of the same thing and that a certain amount of mass can be converted into a tremendous amount of energy and vice versa since the speed of light squared is a very large number.

m=E/c²    equation 1

E=hf

m= h f/ c²    equation 2

c=λ x f

f=c/λ

m=(hc/λ)/c² = h/λc

m=(hc/λ)/c² = h/λv

m=h/λv or λ= h/mv This is often called the De Broglie equation

From De Broglie's equation we now have a way to calculate the wavelength of a so called matter wave that is the wave characteristics of any moving object with which has mass (m) and velocity (v). The quantity mv is simply the momentum of the object in question. So any object no matter its size or mass will exhibit wave characteristics which are dependent on its mass and velocity.

However these effects are so tiny and minuscule when we are dealing with everyday objects e.g. What is the wavelength of a golf ball, mass 100g travelling at 200 m/s?

λ= h/mv = (6.626 x 10^-34)/(0.1 x 200)=3.31 x 10^-34

λ= h/mv = (6.626 x 10^-34)/(9.11 x 10^-31) (2 x 10⁶)
=3.63 x 10^-10

Prior to de Broglie, light was the only known entity exhibiting wave-particle duality. His proposal that particles like electrons could also have wave-like properties extended this concept of wave-particle duality to matter. Shortly after de Broglie's work, Erwin Schrödinger developed the Schrödinger equation, this famous equation incorporated de Broglie's work, allowing for the calculation of the size, shape and energy of orbitals to which electrons are confined to in an atom, these orbitals described the probability of finding the electrons at a specific locations inside the atom.

The Schrödinger equation

The Schrödinger equation is a mathematical equation that is used to describe the behaviour of electrons in atoms using a set of equations called wave functions. These wave functions are like probability maps. They don't pinpoint the exact location of the electrons inside the atom, but instead show the probability of finding the electron in a specific region of space around the nucleus, that is in an orbital. Using this mathematical model of the atom developed by Erwin Schrödinger it is possible to predict with a high probability the location and energy of the electrons within the atom, that is they predict the shapes and energies of the electron orbitals, the volumes in 3d space where the electrons are highly likely to be found.

The Uncertainty principle

There is problem in making measurements of the velocity and location of very small objects such as atoms or electrons. Werner Heisenberg stated in his Uncertainty principle in 1927 that it is impossible to know both the location and the velocity of an electron with complete certainty.

The problem arises when trying to make any sort of observations of the electron, for example if you were trying to measure the position or location of an electron at an exact time then photons of energy would have to somehow interact with the electron in order for you to make some kind of measurement on it. This would transfer energy to the electron and increase its velocity, so the very act of trying to determine its position would cause this to change.

The Uncertainty principle states that we cannot know the electrons position and velocity (or momentum) beyond a certain level of precision. If we know one property accurately then the other will be known less accurately. The principle is often stated as:

(Δx)(Δmv)  ≥ h/4π

(Δx)(Δmv)  ≥  h/4π

Δx  ≥  h /4π(Δmv) = 6.626 x 10^-34/4(3.14)(9.11 x 10^-31)(1.3 x 10⁶)
  ≥ 4.45 x 10^-11 m